Informal Proof of the Pythagorean Theorem

Examples, videos, and solutions to help Grade 8 students learn the Pythagorean theorem and an informal proof of the theorem.

New York State Common Core Math Module 2, Grade 8, Lesson 15

Worksheets for Grade 8

Lesson 15 Student Outcomes

• Students will know the Pythagorean theorem and be shown an informal proof of the theorem.
• Students will use the Pythagorean theorem to find the length of the hypotenuse of a right triangle.

Lesson 15 Summary
Given a right triangle ABC with being the vertex of the right angle, then the sides AC and BC are called the legs of △ ABC and AB is called the hypotenuse of △ ABC. Take note of the fact that side a is opposite the angle A, side b is opposite the angle B, and side c is opposite the angle C. The Pythagorean theorem states that for any right triangle, a² + b² = c².

Classwork
Concept Development
The Pythagorean theorem is a famous theorem that will be used throughout much of high school mathematics. For that reason, you will see several proofs of the theorem throughout the year and have plenty of practice using it. The first thing you need to know about the Pythagorean theorem is what it states:
Pythagorean theorem: If the lengths of the legs of a right triangle are a and b, and the length of the hypotenuse is c, then a² + b² = c².
Given a right triangle ABC with C being the vertex of the right angle, then the sides AC and BC are called the legs of △ ABC and AB is called the hypotenuse of △ ABC.

Discussion
The first proof of the Pythagorean theorem that you will see requires you to know some basic facts about geometry:

1. Congruent triangles have equal areas.
   
2. Triangles can be considered congruent using the Side-Angle-Side Criterion (SAS).
   
3. The triangle sum theorem. (∠ sum of △)
   a. All corresponding parts of congruent triangles are congruent.
   b. For right triangles, the two angles that are not the right angle have a sum of 90°. (∠ sum of △)

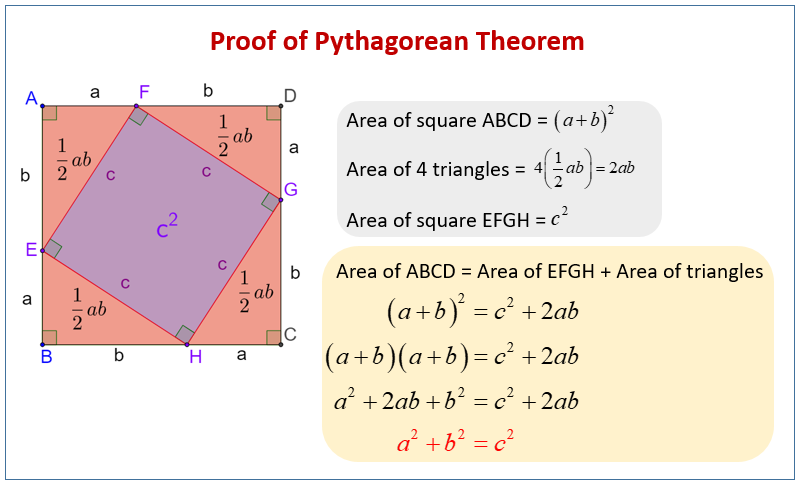
The following diagram shows a proof for the Pythagorean Theorem. Scroll down the page for more examples and solutions on how to use the Pythagorean Theorem.


 

Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets

Deriving the Equation:
We can calculate the total area of the large square in two different ways:

1. Area of the Large Square using its side length
   The side length of the large square is (a + b)
   Area of square = (a + b)² = a² + 2ab + b²
   

2. Area of the Large Square as the sum of its parts
   The large square is composed of:
   Four identical right-angled triangles
   One smaller square in the center
   
   Area of one right triangle = ½ab
   Area of four right triangles = 4(½ab) = 2ab
   Area of the inner square = c²
   Area of square = 2ab + c²
   
   Equating the Two Areas:
   a² + 2ab + b² = 2ab + c²
   a² + b² = c²
   

Conclusion:
This proof visually demonstrates that the relationship a² + b² = c² must hold true for any right-angled triangle.

Example 1
Now that we know what the Pythagorean theorem is, let’s practice using it to find the length of a hypotenuse of a right triangle.
Determine the length of the hypotenuse of the right triangle.

Example 2
Determine the length of the hypotenuse of the right triangle.

Exercises 1–5
For each of the exercises, determine the length of the hypotenuse of the right triangle shown. Note: Figures not drawn to scale.

• Show Video Solutions

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.