Implicit Differentiation

Related Pages
Calculus: Derivatives
Calculus: Derivative Rules
Calculus Lessons

Some functions can be described by expressing one variable explicitly in terms of another variable.

For example:
y = x² + 3
y = x cos x

However, some equations are defined implicitly by a relation between x and y.

For example:
x² + y² = 16
x² + y² = 4xy

We do not need to solve an equation for y in terms of x in order to find the derivative of y. Instead, we can use the method of implicit differentiation. This involves differentiating both sides of the equation with respect to x and then solving the resulting equation for y'.

Example:
If x² + * y*² = 16, find

Solution:
Step 1: Differentiate both sides of the equation

 

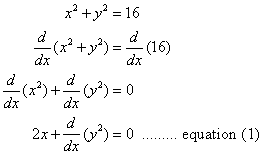
Step 2: Using the Chain Rule, we find that

 

Step 3: Substitute equation (2) into equation (1)

 

Step 4: Solve for

 

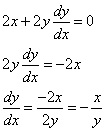
Example:
Find y’ if x³ + y³ = 6xy

Solution:

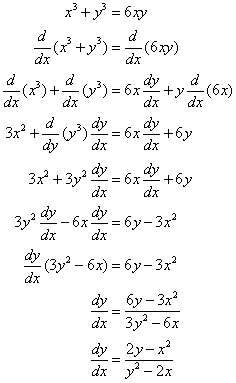
Implicit Differentiation - Basic Idea and Examples
What is implicit differentiation?

The basic idea about using implicit differentiation

1. Take derivative, adding dy/dx where needed.
2. Get rid of parenthesis.
3. Solve for dy/dx

Examples:
Find dy/dx.
x² + xy + cos(y) = 8y

• Show Video Lesson

Implicit Differentiation

Examples:

1. Find dy/dx
   1 + x = sin(xy²)
2. Find the equation of the tangent line at (1, 1) on the curve x² + xy + y² = 3

• Show Video Lesson

Examples of Implicit Differentiation

1. x³ + y³ = xy
2. (x²y) + (xy²) = 3x

• Show Video Lesson

How to use Implicit Differentiation to find a Derivative?
Find the second derivative using implicit differentiation
Find yⁿ for:
9x² + y² = 9

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.