Congruent Triangles - Hypotenuse Leg Theorem

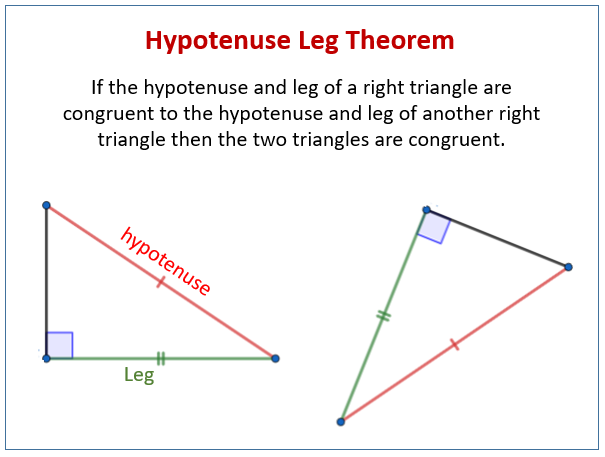
Hypotenuse Leg Theorem

The Hypotenuse-Leg (HL) Theorem is a criterion used to prove the congruence of two right triangles. It’s a special case of congruence postulates that applies only to right triangles.

The following diagram shows the Hypotenuse Leg Theorem. Scroll down the page for more examples and solutions of how to use the Hypotenuse Leg Theorem.

 

Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets

Statement of the HL Theorem:

If the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the two right triangles are congruent.

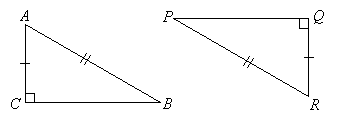
In the following right triangles ΔABC and ΔPQR , if AB = PR, AC = QR then ΔABC ≡ ΔRPQ .

Example:
State whether the following pair of triangles are congruent. If so, state the triangle congruence and the postulate that is used.

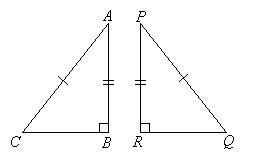
Solution:
From the diagram, we can see that

• ΔABC and ΔPQR are right triangles
• AC = PQ (hypotenuse)
• AB = PR (leg) So, triangle ABC and triangle PQR are congruent by the Hypotenuse Leg Theorem.

Conditions for Applying the HL Theorem:
For the HL Theorem to be used, you must meet three specific conditions:

1. Both triangles must be RIGHT TRIANGLES. This is crucial. If they are not right triangles, you cannot use HL. This means you must explicitly know that they each contain a 90-degree angle.
2. The hypotenuses of both triangles must be congruent. The hypotenuse is the side opposite the right angle, and it’s always the longest side in a right triangle.
3. One pair of corresponding legs of the triangles must be congruent. A leg is one of the two sides that form the right angle. It doesn’t matter which pair of legs (the “short” leg or the “long” leg, if they are different lengths), as long as a corresponding pair is congruent.

Hypotenuse - Leg Congruence Theorem

The hypotenuse-leg congruence theorem states that if the hypotenuse and leg of one right triangle are congruent to the hypotenuse and leg of another right triangle, the two triangles are congruent.
Explains why HL is enough to prove two right triangles are congruent using the Pythagorean Theorem.

• Show Video Lesson

Examples of the Hypotenuse Leg (HL) Theorem and the Angle-Angle-Side (AAS) Theorem
State whether or not the following pairs of triangles must be congruent. If so, state the triangle congruence and name the postulate that is used.

• Show Video Lesson

Prove Triangle Congruence with HL Postulate

HL Postulate (Lesson)
A lesson and proof of the HL (Hypotenuse-Leg) postulate using a two-column proof

• Show Video Lesson

HL Postulate (Practice)

Practice problems and proofs using the HL (Hypotenuse-Leg) Postulate

• Show Video Lesson

In summary:
The HL Theorem is a powerful shortcut for proving right triangle congruence, reducing the need to show all three sides or a combination of sides and angles, as long as you’ve established the specific conditions of a right angle, congruent hypotenuses, and one pair of congruent legs.

Check out our most popular games!

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.