Graphing Parabolas
Related Topics:
More Lessons for Intermediate Algebra or Algebra II
Math Worksheets
A series of free, online Intermediate Algebra Lessons or Algebra II lessons.
Videos, worksheets, and activities to help Algebra students.
In this lesson, we will learn
- the shape of a parabola Click here
- how to find the vertex of a parabola by completing the square Click here
- how to find the vertex of a parabola by using the vertex formula Click here
- how to find the intercepts, domain, range and vertex of a parabola Click here
- how to find the maximum or minimum of a quadratic Click here
The following diagram shows the shape of a parabola and how to find the vertex of a parabola given the equation in general form or vertex form. Scroll down the page for more examples and solutions.
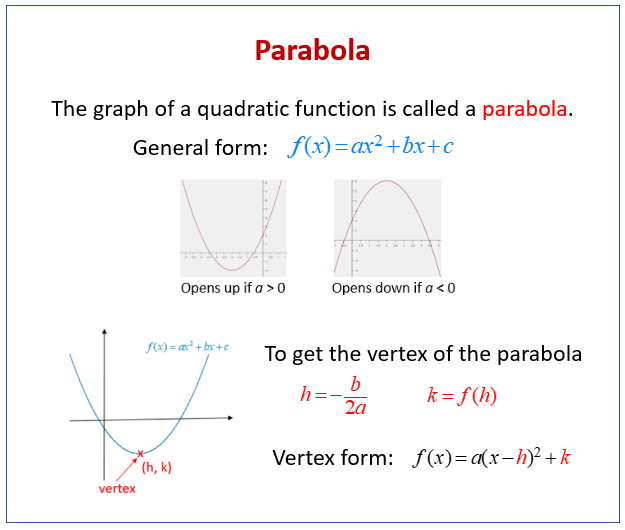
Introduction to Parabolas
When graphing a quadratic equation, the resulting shape is not a straight line, but instead a shape called a parabola. Parabolas vary in direction and shape. The lowest or highest point in a parabola is called a vertex, which lies on the axis of symmetry. If the leading coefficient of the term to the second degree is positive, the parabola faces up. If it is negative, the parabola faces down.
How to talk about a parabola?
Finding the Vertex of a Parabola by Completing the Square
In order to graph a parabola, we need to find several pieces of information, including the vertex. One way to find the vertex of a parabola is to turn the standard form of the quadratic equation into vertex form by completing the square. The primary difference between solving a quadratic by completing the square and putting an equation into vertex form is substituting a “y” for the “0” in the initial equation.
Completing the Square and Vertex Form of Quadratic Equations
How to complete the square and vertex form of quadratic equations is explained.
How you can use the method of completing the square to rewrite a quadratic function?
In the new form, called the vertex form, the vertex can be read from looking at specific numbers.
Finding the Vertex of a Parabola by using the Vertex Formula
The vertex formula is used to determine the vertex of a parabola when the quadratic function is written in general form
Using the vertex formula to find the vertex of a parabola
Finding Intercepts, Domain, Range and Vertex of a Parabola
When graphing and describing the characteristics of a parabola, it is important to know several key pieces of information. The parabola intercepts describe where the parabola intersects the x-axis and the y-axis while the vertex of a parabola is the highest (or lowest) point of the parabola. Knowing the domain and range of a parabola is also helpful when graphing.
In this lesson, students learn to graph quadratic functions that are written in f(x) = ax2 + bx + c form, using the vertex, the y-intercept, and the x-intercepts. The x-coordinate of the vertex can be found using the formula “-b/2a”, and the y-coordinate of the vertex can be found by substituting the x-coordinate of the vertex into the function for x. The y-intercept is equal to “c”, and the x-intercepts can be found by substituting a 0 into the function for f(x). Note that students are also asked to write the equation of the axis of symmetry of the given function, and find the domain, range, and maximum or minimum.
Finding the Maximum or Minimum of a Quadratic
Quadratic graphs have several properties such as shape, vertex and direction that help us solve several types of application questions. The vertex, the quadratic minimum and the quadratic maximum are also helpful when answering problems associated with area, speed and direction. We find the minimum if the parabola opens “up” and the maximum if the parabola opens “down.”
** Maximum and Minimum Values of Quadratic Functions**
This video shows how to find the maximum or minimum value of a quadratic function using the formula for the vertex: (-b/(2a), f(-b/(2a))
How to find the minimum or maximum of a quadratic function?
It also talks about finding the domain and range for those functions. Two examples are included.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.