Geometric Constructions
Related Topics:
More Lessons for High School Geometry
More Lessons for Geometry
Math Worksheets
A series of free, online High School Geometry Video Lessons and solutions.
Videos, worksheets, and activities to help Geometry students.
In these lessons, we will learn
- how to define and construct an angle bisector Click here
- how to define and construct parallel lines Click here
- how to define and construct the altitude of a triangle Click here
- how to define and construct the median of a triangle Click here
The following diagram shows how to construct the altitude of a triangle from a vertex. Scroll down the page for more examples and solutions.
Construct an Angle Bisector
An angle is formed by two rays with a common endpoint. The angle bisector is a ray or line segment that bisects the angle, creating two congruent angles. To construct an angle bisector you need a compass and straightedge. Bisectors are very important in identifying corresponding parts of similar triangles and in solving proofs.
How to define and construct an angle bisector.
This video shows how to bisect an acute angle with a compass and straight edge. The process is the same for an obtuse angle.
Constructing Parallel Lines
Constructing parallel lines with a compass and straightedge uses the converse of the parallel lines theorem. Creating congruent corresponding angles (or congruent AIA or AEA) guarantees parallel lines. The first step in constructing parallel lines is to draw a transversal through the given point to intersect the given line. Last, duplicate an angle created by the transversal and the given line.
using compass and straightedge to construct parallel lines
Instructions on how to construct a line parallel to a given line through a given point.
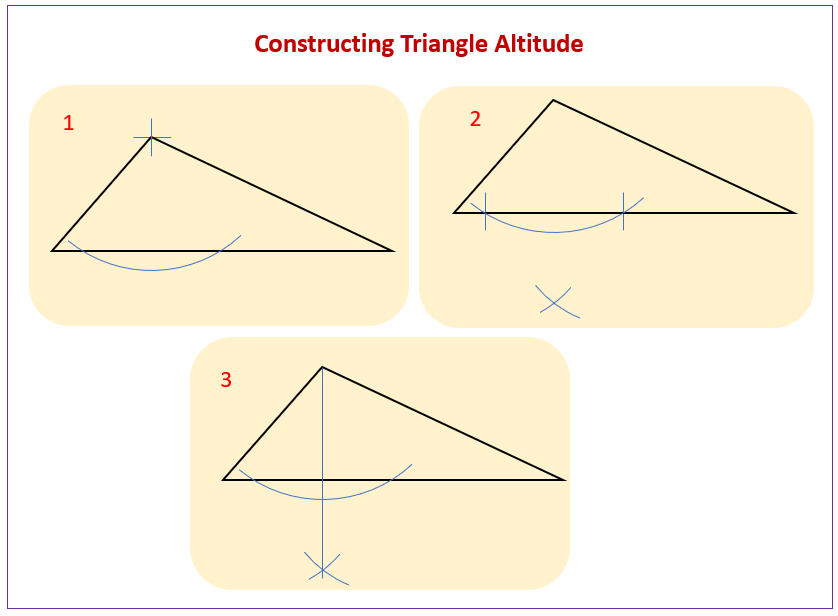
Constructing Triangle Altitude
Altitudes are defined as perpendicular line segments from the vertex to the line containing the opposite side. In each triangle, there are three triangle altitudes, one from each vertex. In an acute triangle, all altitudes lie within the triangle. In a right triangle, the altitude for two of the vertices are the sides of the triangle. In an obtuse triangle, the altitude from the largest angle is outside of the triangle.
Use a compass and a straight edge to create the altitudes of an obtuse triangle. One of the altitude will lie inside the triangle and other two altitudes will lie outside the triangle.
Constructing a Median
A median is a line segment from the vertex to the midpoint of the opposite side in a triangle. In every type of triangle, the median will be contained within the polygon, unlike altitudes which can lie outside the triangle. When constructing a median, we first find the midpoint of the side opposite the desired vertex, then use a straightedge to connect the midpoint and the vertex.
How to define a median in a triangle.
This video will show you how to construct a midpoint using a compass. It will show you how to construct the three medians of an acute triangle.
Using a straight edge and compass constructing a median of a triangle.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.