Frequency Tables, Mean & Measures of Central Tendency
Videos, solutions, worksheets, stories, and songs to help Grade 6 students learn about the frequency tables, mean and measures of central tendency.
The following diagram shows how to the mean from a frequency table. Scroll down the page for more examples and solutions.
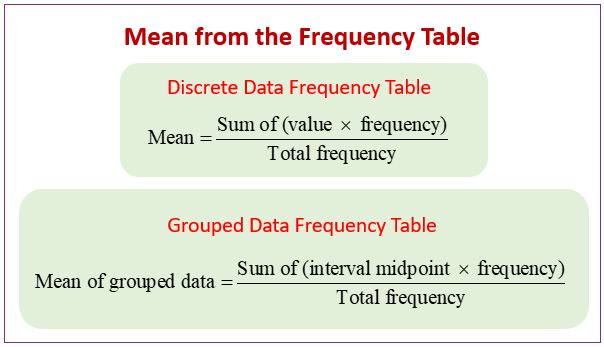
Find the mean from a frequency table
How to find the mean, median, mode, range and interquartile range from a frequency table?
Frequency tables and dot plots
How to organize data into frequency tables and dot plots (or line plots)?
Central Tendency, Frequency Tables and Dot Plots
How to find the mean of a set of data?
One measure of the center of a data set is the mean. It is the sum of the data values divided by the number of data values.
Example:
Find the mean of 12, 34, 56, 78 and 90
How to find the median of a set of data?
Another measure of the center of a data set is the median. It is the middle value of the data when the data are arranged from the least to the greatest.
Examples:
a) Find the median of the values 48, 34, 56, 28, and 60.
b) Find the median of the values 26, 15, 9, 85, 70, 31, 44, and 6.
How to draw frequency tables and dot plots?
Frequency tables and dot plots are used to organize and summarize data.
Example:
The data show the number of hours spent by 20 students in preparation for a final examination. Summarize the data in a frequency table and draw a dot plot.
Frequency Tables and Measures of Central Tendency
Example:
The data below shows the ages of twenty people when they got their driver’s licenses.
a) Make a frequency table and identify the outlier in the data set.
b) Find the mean, median, and mode of the data set.
c) Determine how the outlier affects the mean, median, and mode of the data set.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.