Fractions - Grade 4

Related Pages
Fraction Of A Group
Fraction Word Problems
More Grade 4 Math Lessons
Fraction Worksheets
Fraction Games

Videos, examples, solutions, worksheets, songs, and activities to help Grade 4 students understand fractions.

Fractions
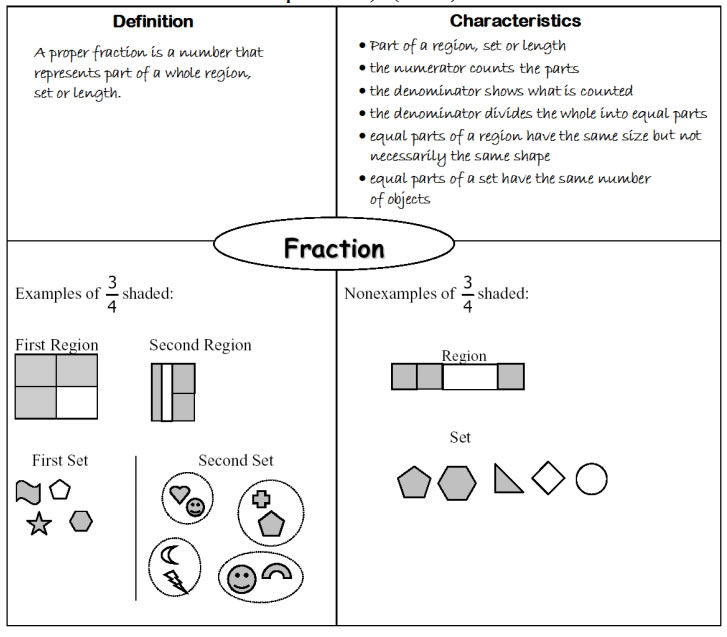
Definition:
A proper fraction is a number that represents part of a whole region, set or length.

Characteristics:

• part of a region, set or length
• the numerator counts the part
• the denominator shows what is counted
• the denominator divides the whole into equal parts
• equal parts of a region have the same size but not necessarily the same shape
• equal parts of a set have the same number of objects

The following diagram shows a sample Frayer Model of a fraction. Scroll down the page for more examples and solutions about fractions.

Comparing Fractions
Fractions can only be compared if the whole is known in each situation. When fractions have the same denominator, the one with the larger numerator is greater.

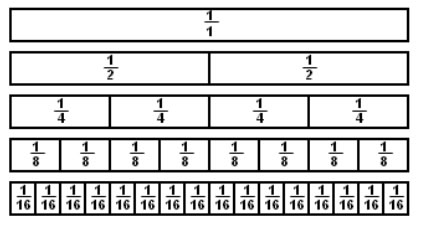
A unit fraction has a numerator 1. Therefore with a unit fraction, the larger the denominator the smaller the fraction part.

The following diagram shows some examples of unit fractions. Scroll down the page for more examples and solutions on using unit fractions for comparing fractions.

Compare fractions using a benchmark fraction
In this lesson, you will learn how to compare fractions with different numerators and denominators to the benchmark fraction of one half by using number lines.

Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as 1/2. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with greater than, less than and equal symbols, and justify the conclusions, e.g., by using a visual fraction model.

• Show Video Lesson

Compare fractions using benchmarks
How to compare fractions with different numerators and denominators to the benchmark fraction of 1/2 by using area models?

Examples:

1. Zach made a popcorn snack. He mixed 5/8 gallon of popcorn with 1/2 gallon of dried apple rings. Did he use more dried apple rings or more popcorn?

2. How can you compare 5/8 and 1/2 without using a model?
   A benchmark is a known size or amount that helps you understand a different size or amount. You can use 1/2 as a benchmark to help you compare fractions.

3. Erika ran 3/8 mile. Maria ran 3/4 mile. Who ran farther?

• Show Video Lesson

Comparing Fractions Using 1/2 As A Benchmark
How to compare fractions with different numerators and denominators to the benchmark fraction of one half by using area models?

• Show Video Lesson

Use Benchmark Fractions to Compare and Order
How to compare fractions to benchmarks like 1/2 to determine size and order?

Examples:

1. A recipe for granola uses 5/8 cup of raisins and 1/6 cup of dried cranberries. Is there a greater amount of raisins or cranberries?

2. List 7/8, 1/2, and 1/3 in order from least to greatest.

3. Use a benchmark fraction to compare. Use >, <, or =.
   

Equivalent Fractions
Understand and explain equivalent fractions using area models and numbers

• Show Video Lesson

Equivalent Fractions - 4th grade
Using a pizza scenario.

• Show Video Lesson

Solve a problem with equivalent fractions
Example:
Anna placed candles on 3/6 of a set of cupcakes. Which fraction is equivalent 3/6?

• Show Video Lesson

Equivalent Fractions Song
Lyrics:
If there were four socks to wear,
Then we would say there’d be two in each pair;
And one of the two pairs, we can declare,
Equals two fourths of all the socks there.
Drawing one half and two fourths on a number line
Shows they can be described with an equal sign;
An equal value is what they’re worth,
So we say one half is equivalent to two fourths.
Equivalent fractions is the name
For fractions whose values are the same.
If the numerator and denominator share a common factor,
Then you can divide the top and bottom by the same number.
On top and under, and say with satisfaction,
“We found an equivalent fraction.”
And you can multiply the top and the bottom
By the same number on top and under,
Which is really a fraction whose value equals one,
And through this action we found an equivalent fraction!

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.