Simplifying Expressions with Exponents

What are Exponents?
An exponent (also called a power or index) tells you how many times to multiply a base number by itself.

Why Use Laws of Exponents? These laws help us simplify expressions that look complicated into simpler forms, making them easier to work with, especially in equations and functions.

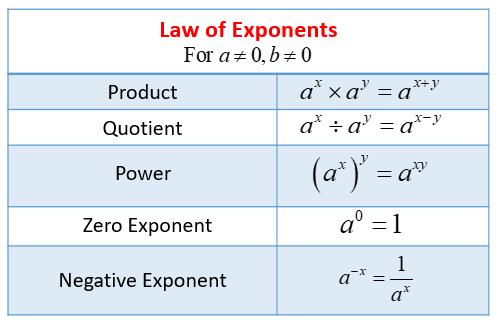
The following diagram shows the law of exponents: product, quotient, power, zero exponent and negative exponent. Scroll down the page for more examples and solutions on how to use the law of exponents to simplify expressions.

 

Exponents Worksheets
Practice your skills with the following Exponents worksheets:
Printable & Online Exponents Worksheets

Law of Exponents
Assume \(a\) and \(b\) are bases (numbers or variables) and \(m\) and \(n\) are exponents (numbers).

1. Product of Powers Law
When multiplying powers with the same base, add the exponents.
Formula: \(a^m \cdot a^n = a^{m+n}\)

2. Quotient of Powers Law
When dividing powers with the same base, subtract the exponents.
Formula: \(\frac{a^m}{a^n} = a^{m-n}\) (where \(a \neq 0\))

3. Power of a Power Law
When raising a power to another power, multiply the exponents.
Formula: \((a^m)^n = a^{mn}\)

4. Power of a Product Law
When raising a product to a power, raise each factor in the product to that power.
Formula: \((ab)^m = a^m b^m\)

5. Power of a Quotient Law
When raising a quotient (fraction) to a power, raise both the numerator and the denominator to that power.
Formula: \((\frac{a}{b})^m = \frac{a^m}{b^m}\) (where \(b \neq 0\))

6. Zero Exponent Law
Any non-zero base raised to the power of zero is 1.
Formula: \(a^0 = 1\) (where \(a \neq 0\))

7. Negative Exponent Law
A negative exponent means the reciprocal of the base raised to the positive exponent.
Formula: \(a^{-n} = \frac{1}{a^n}\) (where \(a \neq 0\))

8. Fractional Exponent Law (Radicals)
A fractional exponent indicates a root.
Formula: \(m^\frac{m}{n} = \sqrt[n]{a^m} = (\sqrt[n]{a})^m\)

Combining Laws to Simplify Expressions
Often, you’ll need to use several laws in one problem. Follow the order of operations (PEMDAS/BODMAS), addressing parentheses/brackets and exponents first.

Simplifying expressions using the Laws of Exponents
We can use what we know about exponents rules in order to simplify expressions with exponents. When simplifying expressions with exponents we use the rules for multiplying and dividing exponents, and negative and zero exponents.

• Show Video Lesson

Simplifying expressions with exponents
2 examples of simplifying expressions using exponent properties

• Show Video Lesson

Simplify exponential expressions, several rules

• Show Video Lesson

Simplifying Exponential Expressions

• Show Video Lesson

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.