Graphing Exponential Functions
In this lesson, we will learn
- how to graph exponential functions by plotting points.
- the characteristics of graphs of exponential functions.
- how to use transformations to graph an exponential function.
Graph exponential functions by plotting points
The general form of an exponential function is y = bn, where b > 0 and b ≠ 1 and n is a real number.
Example:
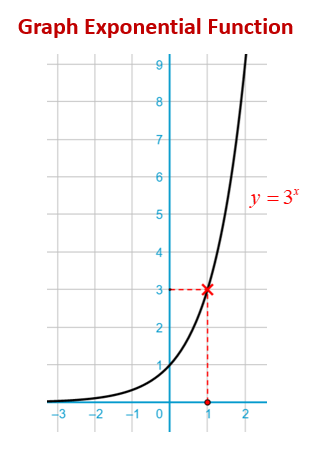
Draw the graph of y = 3x for –1 ≤ x ≤ 2.
Solution:
x |
–1 |
–0.5 |
0 |
0.5 |
1 |
1.5 |
2 |
y |
0.33 |
0.58 |
1 |
1.73 |
3 |
5.2 |
9 |
The following diagram shows the graph of the exponential function y = 3x. Scroll down the page for more examples and solutions on how to graph exponential functions.
In this video, we look at how to graph an exponential function by plotting points.
Characteristics of Exponential Graph
From the graph above, we notice the following characteristics or properties of the exponential graph (curve) y = bn, where* b* > 0 and *b* ≠ 1 and *n* is a real number:
a) As the value of *x* increases, the value of *y* increases far more than the increase of value of *x*.
b) The range (or values of *y*) are positve real numbers (never zero).
c) The graph is asymptotic to the *x*-axis that is it gets very close to the *x*-axis but does not touch it or cross it.
d) The graph always crosses the *y*-axis at (0, 1)
This video gives the properties of exponential functions (where b >1).
This video gives the properties of exponential functions (where 0 < b <1).
Use transformations to graph an exponential function
The following video shows how to use transformations to graph an exponential function.
How to graph exponential functions that have been transformed (shifted up or down, left or right, and perhaps even reflected)?
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.