Edexcel Core Mathematics C34 January 2015
Related Topics:
More videos, activities and worksheets that are suitable for A Level Maths
Questions and Worked Solutions for C34 Edexcel Core Mathematics January 2015.
Edexcel Core Mathematics C34 January 2015 Past Paper
Core 34 Mathematics Edexcel January 2015 Question 1
The curve C has equation
y = (3x - 2)/(x - 2)2, x ≠ 2
The point P on C has x coordinate 3
Find an equation of the normal to C at the point P in the form ax + by + c = 0, where a, b and c are integers.
Core 34 Mathematics Edexcel January 2015 Question 2
Solve, for 0 ≤ θ < 2π,
2cos2θ = 5 – 13sinθ
Give your answers in radians to 3 decimal places.
(Solutions based entirely on graphical or numerical methods are not acceptable.)
Core 34 Mathematics Edexcel January 2015 Question 3
The function g is defined by
g : x ↦ 6|8 – 2x|, x ∈ ℝ , x ≥ 0
(a) Sketch the graph with equation y = g(x), showing the coordinates of the points where the graph cuts or meets the axes.
(b) Solve the equation
|8 – 2x| = x + 5
The function f is defined by
f : x ↦ x2 – 3x + 1, x ∈ ℝ , 0 ≤ x ≤ 4
(c) Find fg(5).
(d) Find the range of f. You must make your method clear.
Core 34 Mathematics Edexcel January 2015 Question 4
Use the substitution x = 2sinθ to find the exact value of
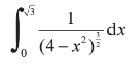
Core 34 Mathematics Edexcel January 2015 Question 5
Core 34 Mathematics Edexcel January 2015 Question 6(i)
(i) Given x = tan24y, 0 < y < π/8, find dy/dx as a function of x.
Write your answer in the form 1/A(xp + xq), where A, p and q are constants to be found.
(ii) The volume V of a cube is increasing at a constant rate of 2 cm3 s-1. Find the rate at which the length of the edge of the cube is increasing when the volume of the cube is 64 cm3.
Core 34 Mathematics Edexcel January 2015 Question 7
(a) Given that
2cos(x + 30)° = sin(x - 30)°
without using a calculator, show that
tan x° = 3√3 - 4
(b) Hence or otherwise solve, for 0 ≤ θ < 180,
2cos(2θ + 40)° = sin(2θ - 20)°
Give your answers to one decimal place.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.