Edexcel Core Mathematics C2 June 2011
Related Topics:
More videos, activities and worksheets that are suitable for A Level Maths
Questions and Step-by-Step Solutions for C2 Edexcel Core Mathematics June 2011.
Edexcel Core Mathematics C2 June 2011 Past Paper
C2 Mathematics Edexcel June 2011 Question 6
6. The second and third terms of a geometric series are 192 and 144 respectively. For this series, find
(a) the common ratio,
(b) the first term,
(c) the sum to infinity,
(d) the smallest value of n for which the sum of the first n terms of the series exceeds 1000.
6 (a)(b) Geometric Series
6(c) Sum of Series
6 (d)
C2 Mathematics Edexcel June 2011 Question 7
7. (a) Solve for 0 ≤ x < 360°, giving your answers in degrees to 1 decimal place,
3sin(x + 45°) = 2
(b) Find, for 0 ≤ x 2π, all the solutions of
2sin2x + 2 = 7cosx
giving your answers in radians.
You must show clearly how you obtained your answers.
7 (b)
C2 Mathematics Edexcel June 2011 Question 8
A cuboid has a rectangular cross-section where the length of the rectangle is equal to twice its width, x cm, as shown in Figure 2.
The volume of the cuboid is 81 cubic centimetres.
(a) Show that the total length, L cm, of the twelve edges of the cuboid is given by
L = 12x + 162/x2
(b) Use calculus to find the minimum value of L.
(c) Justify, by further differentiation, that the value of L that you have found is a minimum.
8 (b)
8 (c)
C2 Mathematics Edexcel June 2011 Question 9
The straight line with equation y = x + 4 cuts the curve with equation y = −x2 + 2x - 24 at the points A and B, as shown in Figure 3.
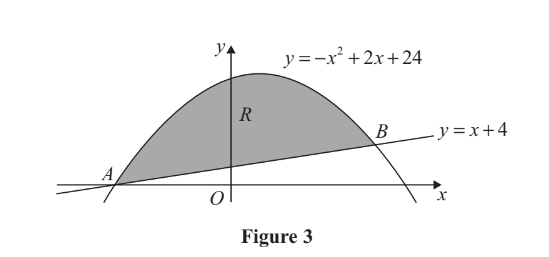
(a) Use algebra to find the coordinates of the points A and B.
The finite region R is bounded by the straight line and the curve and is shown shaded in Figure 3.
(b) Use calculus to find the exact area of R.
9 (b)
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
Penguin Solitaire
Penguin Solitaire is a fun game that aims to move all cards to the foundations to build four full sequences. There are two versions here: Penguin (Tuxedo) and Penguin (Original).
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.