The Number e, Natural Logarithm and Common Logarithm

High School Math based on the topics required for the Regents Exam conducted by NYSED: The Number e and the Natural Logarithm, Common Logarithms and Natural Logarithms, Evaluating Common Logs and Natural Logs Using a Calculator.

The following diagrams show common logarithms and natural logarithms. Scroll down the page for more examples and solutions.

 

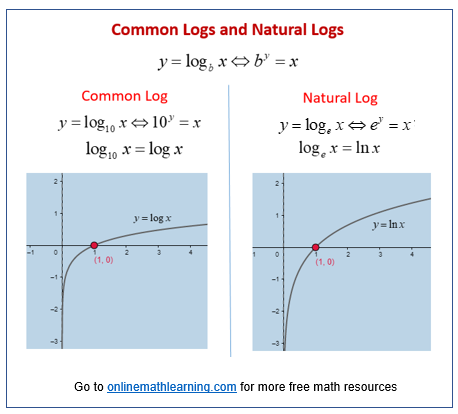
Common Logarithms and Natural Logarithms
We can use many bases for a logarithm, but the bases most typically used are the bases of the common logarithm and the natural logarithm. The common logarithm has base 10, and is represented on the calculator as log(x). The natural logarithm has base e, a famous irrational number, and is represented on the calculator by ln(x). The natural and common logarithm can be found throughout Algebra and Calculus.

The Number e and the Natural Logarithm
The natural log is the logarithm to the base of the number e and is the inverse function of an exponential function. Natural logarithms are special types of logarithms and are used in solving time and growth problems. Logarithmic functions and exponential functions are the foundations of logarithms and natural logs. This video looks at properties of e and ln and simplifying expressions containing e and natural logs. It includes five examples.

Evaluating Common Logs and Natural Logs Using a Calculator

• Show Step-by-step Solutions

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.