Domain and Range of Functions

Domain and Range of a Function

1. Domain
   The domain of a function is the set of all possible input values (x-values) for which the function is defined.
   
2. Range
   The range of a function is the set of all possible output values (y-values) the function can produce.
   

The following diagrams show the domain and range of a function. Scroll down the page for more examples and solutions.

 

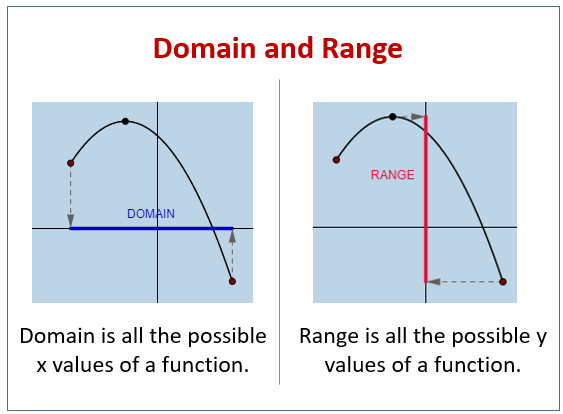
How to find the domain:
Look for values of x that would make the function undefined and exclude that from the domain.

1. The denominator of a fraction cannot be zero. If your function has a variable in the denominator, set the denominator equal to zero and exclude those values of x from the domain.
2. You cannot take the square root (or any even root, like fourth root, sixth root, etc.) of a negative number in the set of real numbers. If your function has an even root, set the expression inside the root to be greater than or equal to zero and solve for x
3. The argument of a logarithm (the number inside the log) must be strictly positive.
4. If none of the above restrictions apply, such as with most polynomial functions, the domain is typically all real numbers, represented as (−∞,∞).

How to find the range:

1. For parabolas: If a>0, the parabola opens upwards, and the minimum y-value is at the vertex. If a<0, it opens downwards, and the maximum y-value is at the vertex. The range will be from the vertex’s y-coordinate to infinity (or negative infinity to the vertex’s y-coordinate).
2. For square root functions: The square root symbol √ (by convention) always denotes the principal (non-negative) square root. So the range is [0,∞).
3. For absolute value functions: The output of an absolute value function is always non-negative. So the range is [0,∞)
4. Visually inspect the graph of the function. The range corresponds to the portion of the y-axis that the graph covers. Look for the lowest and highest y-values the graph reaches.
5. The range of a function is the domain of its inverse function. Find the inverse function (f^-1(x)) and then find the domain of (f^-1(x)).

Videos

Domain and Range

How to find the domain and range?

An important part of understanding functions is understanding their domain and range. Domain and range are all the possible x-values and y-values of the function, and can often be described easily by looking at a graph. In order to grasp domain and range, students must understand how to determine if a relation is a function and interpreting graphs.

This video provides two examples of how to determine the domain and range of a function given as a graph.

• Show Video Lesson

Examples of how to determine the domain and range of a function given as a graph

• Show Video Lesson

How to Find the Domain & Range of a Function

Finding the domain and range of a function is as simple as finding the possible X and Y values, respectively.
Learn about X and Y values as dependent and independent variables.

• Show Video Lesson

Finding the Domain of a Function Algebraically

Finding the domain of a function, without graphing.

Restrictions:

1. No zero in the denominator of a fraction.
2. No negative numbers under square roots after simplifying.

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.