Function Notation

What is a Function?
A function is a rule that assigns exactly one output to each input. In other words, for every input x, there is exactly one corresponding output y.

What is function notation?
Functions are given letter names.
The names are of the form f(x) which is read “f of x”. The letter inside the parentheses, usually x, stands for the domain set.

The entire symbol, usually f(x), stands for the range set.

The ordered-pair numbers become (x, f(x)).

The following diagram shows what is function notation. Scroll down the page for more examples and solutions of function notations.

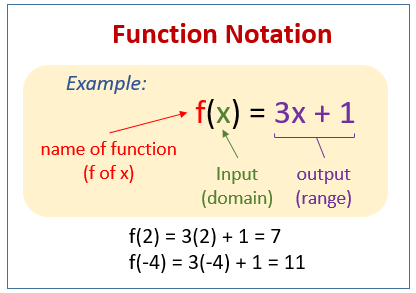
Function notation uses the symbol f(x) to represent the output of a function f when the input is x.
f is the name of the function.
x is the input (independent variable).
f(x) is the output (dependent variable).

Example:
Given f(x) = x² + 3x – 1, find
a) f(1)
b) f(–1)
c) f(a)
d) f(x – 1)

Solution:
a) f(1) = (1)² + 3(1) – 1 = 3
b) f(–1) = (–1)² + 3(–1) – 1 = –3
c) f(a) = a² + 3a – 1
d) f(x – 1) = (x – 1)² + 3(x – 1) – 1
= x² – 2x + 1 + 3x – 3 – 1 = x² + x –3

Example:
Give g(x) = x² + 2, find
a) g(a + b)
b) g(x²)

Solution:
a) g(a + b) = (a + b)² + 2
= a² + 2ab + b² + 2
b) g(x²) = (x²)² + 2 = x⁴ + 2

Videos

Function Notation
Throughout mathematics, we find function notation. Function notation is a way to write functions that is easy to read and understand.
Functions have dependent and independent variables, and when we use function notation the independent variable is commonly x, and the dependent variable is f(x).
In order to write a relation or equation using function notation, we first determine whether the relation is a function.

• Show Video Lesson

Function Notation
How to use the function Notation?
A basic description of function notation and a few examples involving function notation.
Example:
If g(t) = t² - 2t + 1

1. g(3t)
   
2. 5g(-1)
   
3. solve g(t) = 1
   If f(x) = 5x -2, h(x) = x²
   
4. 3f(x)
   
5. f(2x - 1)
   
6. -f(a)
   
7. Solve f(-x) = h(x) + 2

• Show Video Lesson

Why Use Function Notation? (Advantages)

1. Clarity and Specificity:
   It clearly states the input variable. For example, f(x) immediately tells you the function operates on x.
   It’s more precise than just “y”. If you have multiple functions, you can name them differently (e.g., f(x), g(x), h(t)).
   
2. Easy Evaluation:
   It simplifies showing the evaluation of a function for a specific input.
   
3. Directly Shows Input-Output Relationship:
   When you see f(5), you immediately know that 5 is the input value for the function f
   

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.