Divisibility Rules For 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 And 13
Related Pages
Basic Divisibility Rules
Divisibility Rules Explained
Free Math Worksheets
Divisibility rules are shortcuts to determine if a number is evenly divisible by another number without actually performing the division. They’re useful for simplifying fractions, factoring numbers, and mental math.
Lessons with videos, examples, solutions and stories to help Grade 4 students learn the Divisibility Rules for 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13.
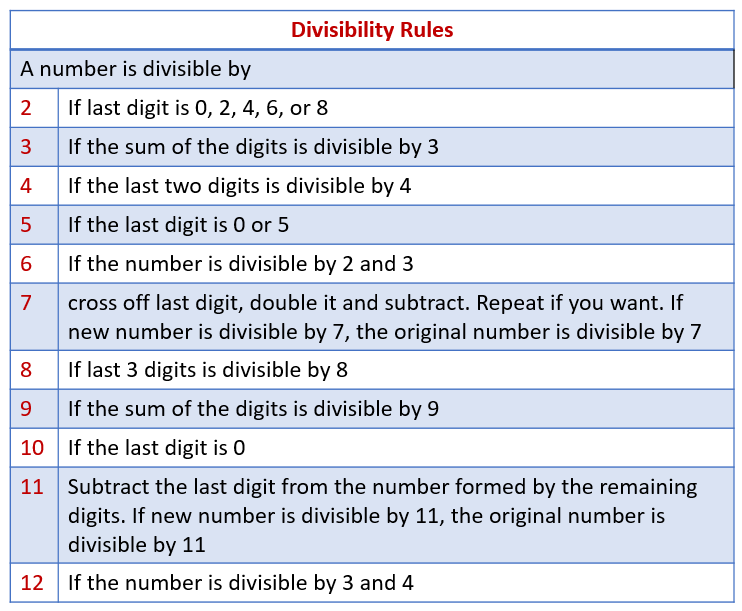
The following table gives the Divisibility Rules for 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12. Scroll down the page for examples and solutions. Divisibility means one number divides into another number and there is not a remainder.
Worksheets/Games to test your knowledge of divisibility rules
Divisibility Game
Divisibility Tests (printable)
Divisibility Rules (online)
Divisibility Tests For 2, 3, 5, 7 And 11
This shows you the divisibility tests for 2, 3, 5, 7, and 11, so you can tell if those numbers are factors of a given number or not without dividing.
- Divisibility Test for 2: The last digit is 0, 2, 4, 6, or 8.
- Divisibility Test for 3: The sum of the digits is divisible by 3.
- Divisibility Test for 5: The last digit is 0 or 5.
- Divisibility Test for 7: Cross off last digit, double it and subtract. Repeat if you want. If new number is divisible by 7, the original number is divisible by 7.
- Divisibility Test for 11: For a 3-digit number, sum of the outside digits minus the middle digit must be 0 or 11.
Basic Divisibility Rules:
Here is the explanation of the divisibility rules for 2, 4, 5, 6, 7, 8, 9, 10, 11, 12 and examples on how to use them to test divisibility.
Divisible by 2:
A number is divisible by 2 if the last digit is even i.e. 0, 2, 4, 6, or 8.
Example:
138 is divisible by 2 because the last digit, 8, is even.
249 is not divisible by 2 because the last digit, 9, is not even.
Divisible by 3:
A number is divisible by 3 if the sum of the digits is divisible by 3.
372 is divisible by 3 because 3+7+2 = 12 and 12 ÷ 3 = 4.
218 is not divisible by 3 because 2+1+8 = 11 and 11 ÷ 3 = 3 2/3.
Divisible by 4:
A number is divisible by 4 if the last two digits are divisible by 4.
312 is divisible by 4 because 12 ÷ 4 = 3.
334 is not divisible by 4 because 34 ÷ 4 = 8 1/2.
Divisible by 5:
A number is divisible by 5 if the digit is 0 or 5.
325 is divisible by 5 because the last digit is 5.
314 is not divisible by 5 because the last digit is, 4, is not 0 or 5.
Divisible by 6:
A number is divisible by 6 if it is even and is divisible by 3.
228 is divisible by 6 because it is even and 2+2+8 = 12 and 12 ÷ 3 = 4.
314 is not divisible by 6 because 3+1+4 = 8 and 8 ÷ 3 = 2 2/3.
Divisible by 7:
Double the last digit and subtract it from a number made by the other digits. The result must be divisible by 7.
364 is divisible by 7 because double 4 is 8, 36 - 8 = 28, and 28 ÷ 7 = 4.
213 is not divisible by 7 because double 3 is 6, 21 - 6 = 15 and 15 ÷ 7 = 2 1/7.
Divisible by 8:
A number is divisible by 8 if the last three digits are divisible by 8.
11816 is divisible by 8 because 816 ÷ 8 = 102.
32113 is not divisible by 8 because 113 ÷ 8 = 14 1/8.
Divisible by 9:
A number is divisible by 9 if the sum of the digits is divisible by 9.
1107 is divisible by 9 because 1+1+0+7 = 9 and 9 ÷ 9 = 1.
2317 is not divisible by 9 because 2+3+1+7 = 13 ÷ 9 = 1 4/9.
Divisible by 10:
A number is divisible by 10 if the number ends in 0.
9870 is divisible by 10 because it ends with 0.
7102 is not divisible by 10 because it does not end with 0.
Divisible by 11:
Add and subtract the digits in an alternating pattern. Then check if the answer is divisible by 11.
2563 is divisible by 11 because 2-5+6-3 = 0.
7213 is not divisible by 11 because 7-2+1-3= 3.
Uses of Divisibility Rules:
Simplifying Fractions: Divisibility rules help you quickly find common factors between the numerator and denominator of a fraction, allowing you to simplify it to its lowest terms.
Example: Simplify 12/18. Both 12 and 18 are divisible by 2, giving 6/9. Both 6 and 9 are divisible by 3, giving 2/3.
Factoring Numbers: When finding the factors of a number, divisibility rules help you quickly identify some of the factors. Example: Find the factors of 36. You know it’s divisible by 2, 3, 4, 6, 9, and so on.
Mental Math: Divisibility rules make it easier to perform mental calculations and estimations.
Example: Quickly checking if 147 is divisible by 3 (1 + 4 + 7 = 12, divisible by 3).
Checking Calculations: You can use divisibility rules to check if your calculations are likely correct. If you expect a result to be divisible by a certain number, you can use the rule to confirm.
Finding Prime Factorization: Divisibility rules are helpful in finding the prime factorization of a number.
Divisibility Tests For 11 And 13
The following lesson goes over two divisibility tests for 11 and also the one for 13.
Divisibility Rules For 2, 3, 4, 5, 6, 8, 9, 10, And 12
Learn the divisibility rules for 2, 3, 4, 5, 6, 8, 9, 10 and 12.
Divisibility Rule Of Six
A number is divisible by 6, if it is divisible by both 2 and 3.
Divisibility Rule Of Ten
A number is divisible by 10 if it ends in a zero.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.