Construct Parallelogram, Square and Rectangle
In these lessons, we will learn
- how to construct a parallelogram given the lengths of its sides and an angle.
- how to construct a parallelogram given the lengths of its diagonals.
- how to construct a square given the length of the diagonal.
- how to construct a square given the length of one side.
- how to construct a rectangle.
Related Pages
More Geometry Lessons
Construct A Parallelogram given sides and angle
Example:
Construct a parallelogram ABCD with sides AB = 4 cm and AD = 5 cm and angle A = 60˚.
Solution:
Step 1: Construct a line segment AB = 4 cm. Construct a 60˚ angle at point A.
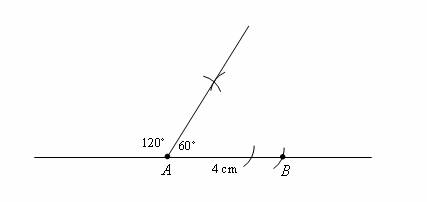
Step 2:
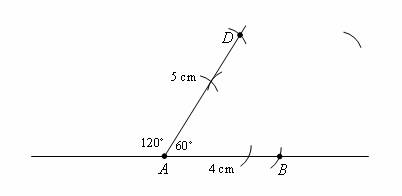
Step 3: Stretch your compasses to 4 cm, place the sharp end at D and draw an arc to intersect the arc drawn in step 2. Label the intersecting point C. Join C to D and B to C to form the parallelogram ABCD.
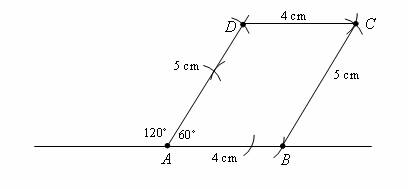
How to construct a parallelogram with a given angle and certain side lengths?
Example:
Construct a parallelogram with side lengths c and d and with a 45° angle.
How to construct a parallelogram, using two lengths and one angle provided?
Step 1: Make a copy of the given angle.
Step 2: Make a copy of the lengths for each side.
Step 3: Use the compass to mark the fourth vertex.
Construct a Parallelogram given its diagonals
This video shows how to construct a parallelogram given the lengths of its diagonals, using the property that diagonals of a parallelogram bisect each other. An infinite number of parallelograms are possible.
Example:
Construct a parallelogram ABCD given the diagonals AC and BD.
Step 1: Bisect AC and BD.
Step 2: Draw a circle with the radius equals to 1/2 of AC.
Step 3: Draw a concentric circle with the radius equals to 1/2 of BD.
Step 4: Mark two points that will form the diameter on the bigger circle.
Step 5: Mark two points that will form the diameter on the smaller circle.
Step 6: Join the four points to form the parallelogram.
How to construct a parallelogram using the intersecting diagonals property of a parallelogram?
The diagonals of a parallelogram bisect each other.
How to construct a square given the length of its diagonal?
The following video shows how to construct a square with a compass and straight edge given the length of a diagonal.
How to construct a square using a diagonal?
How to construct a square given its side?
The following video shows how to construct a square given the length of one side.
How to construct a square given the length of one side? Two methods are shown.
How to construct a rectangle?
How to draw a Rectangle Using a Compass and Straight Edge, and perpendicular bisector constructions.
Construct a rectangle with compass and straight edge.
Step 1: Construct two perpendicular segments.
Step 2: Mark off congruent sides.
Step 3: Check for 4 right right angles.
Step 4: Check that the diagonals are equal in lengths.
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.