Construct the Median of a Triangle
Related Topics:
More Lessons for High School Regents Exam
Math Worksheets
High School Math based on the topics required for the Regents Exam conducted by NYSED.
The following diagram shows the medians of a triangle. Scroll down the page for more examples and solutions of how to construct the median of a triangle.
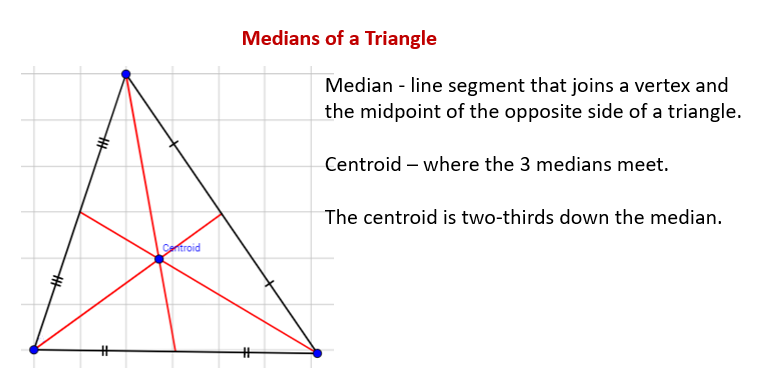
Medians of a Triangle and their properties
The median is a line segment that joins a vertex and the midpoint of the opposite side of a triangle.
A triangle has three medians.
The point of concurrency of the medians is called the centroid.
The centroid is the center of mass of an object of uniform density in the shape of a triangle.
The object will balance on any line through the centroid.
The centroid is two-thirds the distance from the vertices to the midpoint on the opposite side.
Constructing a Median
A median is a line segment from the vertex to the midpoint of the opposite side in a triangle.
In every type of triangle, the median will be contained within the polygon, unlike altitudes which can lie outside the triangle.
When constructing a median, we first find the midpoint of the side opposite the desired vertex, then use a straightedge to connect the midpoint and the vertex.
How to construct the three medians of an acute triangle?
How to construct a midpoint using a compass?
The meeting point of the three medians will form the centroid of the triangle.
Constructing a Median of a Triangle
Using a straight edge and compass constructing a median of a triangle
Constructing a median with a compass
- Open the compass past the estimated midpoint of the side. Strike an arc.
- Keeping the same setting, move to the vertex on the opposite side of the side you are working with.
- Strike an arc such that it intersects the first arc twice.
- Use a straightedge to find the midpoint of the side.
- Draw a segment from that midpoint to the opposite vertex.
Do this for all three sides and you’ll find the centroid of the triangle.
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.