Conic Sections
In these lessons, we will learn
- about conic sections.
- how to graph the equation of a parabola given in standard form and general form.
- how to graph the equation of a circle given in standard form and general form.
- how to graph the equation of an ellipse given in standard form and general form.
A series of free, online video lessons with examples and solutions to help Algebra students learn about parabola conic sections.
Related Pages
Conic Sections
Conic Sections: Circles
Conic Sections: Ellipses
Conic Sections: Hyperbolas
The following diagrams show the conic sections for circle, ellipse, parabola, and hyperbola. Scroll down the page for more examples and solutions on conic sections.
Introduction to Conic Sections
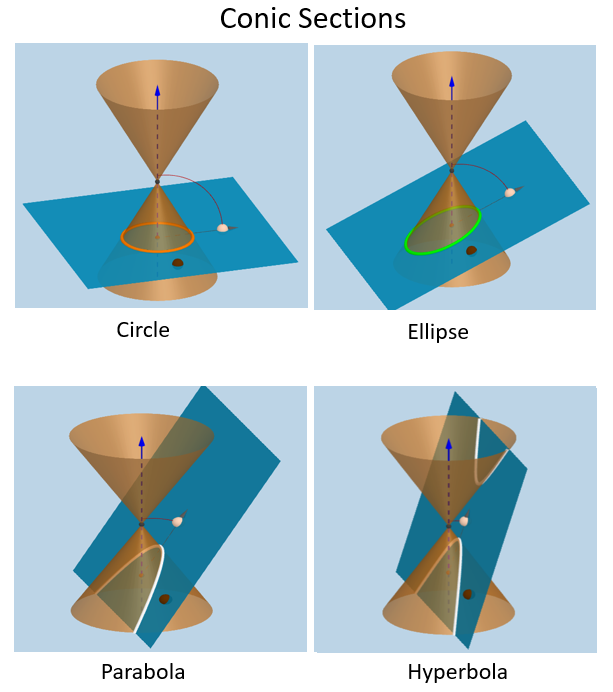
By definition, a conic section is a curve obtained by intersecting a cone with a plane. In Algebra II, we work with four main types of conic sections: circles, parabolas, ellipses and hyperbolas. Each of these conic sections has different characteristics and formulas that help us solve various types of problems.
How to generate a circle, ellipse, parabola, and hyperbola by intersecting a cone with a plane?
Name each of the 4 conics.
Demonstrate how the conics are formed by a plane and a cone.
The fixed line is called the axis of the cone.
The vertex is the point shared by both cones.
The lines that pass through the vertex and form the cones are the generators. The generators lie in the cone.
The cone consists of two parts called the nappes.
A conic section section is a curve generated by intersecting a right circular cone with a plane.
A circle is generated when the plane is perpendicular to the axis of the cone.
An ellipse is generated when the plane is tilted so it intersects each generator, but only intersects one nappe.
A parabola is generated when the plane is tilted so it is parallel to one generator and only intersects one nappe.
A hyperbola is generated when the plane intersect both nappes.
Demonstrate what is a conic section
Conic Section: Parabola
Conic Sections: The Parabola part 1 of 2
Defines a parabola and explains how to graph a parabola in standard form.
Identify the key components to a parabola.
Graph a parabola in standard form.
Conic Sections: The Parabola part 2 of 2
How to graph a parabola given in general form by rewriting it in standard form?
Write the general form of a parabola in standard form.
Graph a parabola.
A parabola is set of all points (x,y) that are equidistant from a fixed line called the directrix and a fixed point called the focus.
Example:
Write the parabola in standard form and then graph.
a) x2 + 8x = 4y - 8
b) y2 + 2y = 8x - 1
Conic Section: Circle
When working with circle conic sections, we can derive the equation of a circle by using coordinates and the distance formula. The equation of a circle is (x - h)2 + (y - k)2 = r2 where r is equal to the radius, and the coordinates (x,y) are equal to the circle center. The variables h and k represent horizontal or vertical shifts in the circle graph.
How to graph a circle in standard form and general form?
Example:
-
Graph the circle.
(x - 3)2 + (y + 2)2 = 16 -
Write in standard form and then graph.
2x2 + 2y2 - 12x + 8y - 24 = 0
Conic Sections: Introduction to Circles
Conic Section: Ellipse
An ellipse is an important conic section and is formed by intersecting a cone with a plane that does not go through the vertex of a cone. The ellipse is defined by two points, each called a focus. From any point on the ellipse, the sum of the distances to the focus points is constant. The position of the foci determine the shape of the ellipse. The ellipse is related to the other conic sections and a circle is actually a special case of an ellipse.
How to talk about an ellipse?
Conic Sections: The Ellipse part 1 of 2
This video defines an ellipse and explains how to graph an ellipse in standard form.
Conic Sections: The Ellipse part 2 of 2
This video explains how to graph an ellipse in general form.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.