Congruent and Similar Figures

Congruent figures and similar figures are two fundamental concepts in geometry that describe relationships between shapes, but they differ in crucial ways regarding size.

Congruent Figures
Definition: Two figures are congruent if they have the exact same shape and the exact same size. One figure can be perfectly superimposed onto the other by using only rigid transformations (translation, rotation, or reflection).
The symbol for congruence is ≅.

Key Properties:
Corresponding angles are equal.
Corresponding side lengths are equal.
All corresponding parts (angles, sides, vertices) are congruent (CPCTC - Corresponding Parts of Congruent Triangles are Congruent).

Similar Figures
Definition: Two figures are similar if they have the exact same shape but potentially different sizes. One figure is an enlargement or reduction of the other.
The symbol for similarity is ~.

Key Properties:
Corresponding angles are equal.
Corresponding side lengths are proportional. This means the ratio of any pair of corresponding sides is constant. This constant ratio is called the scale factor.
The shape is preserved, but the size may change.

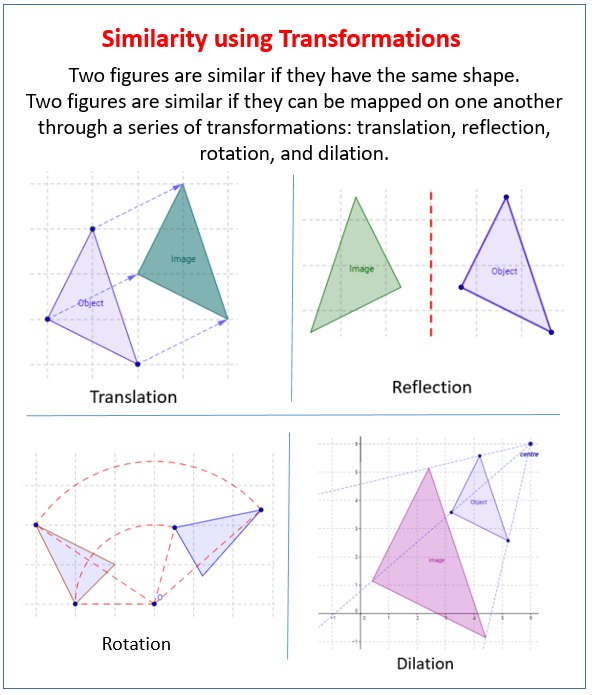
The following diagrams show the similarity transformations: translation, reflection, rotation, and dilation. Scroll down the page for more examples and solutions.

 

Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets

Scale Factor:
If Figure B is similar to Figure A, and a side length in Figure B is L_B and the corresponding side length in Figure A is L_A, then the scale factor \(k = \frac{L_A}{L_B}\).

If k > 1, Figure B is an enlargement of Figure A.
If 0 < k < 1, Figure B is a reduction of Figure A.
If k = 1, Figure B is congruent to Figure A (a special case of similarity).

Similar vs Congruent shapes
Grade 8 Math #10.3b, Dilations
An explanation of the difference between similar and congruent shapes with a pre-image and an image.
What makes two shapes similar but not congruent?

• Show Video Solutions

Testing similarity through transformations
Two figures are similar is they can be mapped on one another through a series of transformations: translation, reflection, rotation, dilation.

• Show Video Solutions

Similar vs. Congruent

• Show Step-by-step Solutions

Congruency and similarity

• Show Video Solutions

Proving Triangle Congruence:
To prove two triangles are congruent, you typically need to show that certain combinations of their corresponding sides and angles are equal:

1. SSS (Side-Side-Side): All three corresponding sides are equal.
2. SAS (Side-Angle-Side): Two corresponding sides and the included angle (the angle between them) are equal.
3. ASA (Angle-Side-Angle): Two corresponding angles and the included side (the side between them) are equal.
4. AAS (Angle-Angle-Side): Two corresponding angles and a non-included side are equal.
5. HL (Hypotenuse-Leg): The hypotenuse and one leg of one right triangle are equal to the hypotenuse and one corresponding leg of another right triangle.

Proving Triangle Similarity:
To prove two triangles are similar, you need to show that corresponding angles are equal or corresponding sides are proportional:

1. AA (Angle-Angle) Similarity: If two angles of one triangle are congruent to two angles of another triangle. (The third angles must also be equal).
2. SSS (Side-Side-Side) Similarity: If the corresponding sides of two triangles are proportional.
3. SAS (Side-Angle-Side) Similarity: If two sides of one triangle are proportional to two corresponding sides of another triangle, and the included angles (the angles between those sides) are equal.

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.