Congruency and Symmetry
In these lessons, we will learn congruence of 2-D shapes and the symmetry of 2-D shapes. This lesson is suitable for Grade 3 and Grade 4 kids.
Related Topics:
More Math Lessons for Grade 4
More Lessons on Geometry
Congruent Math Games
Congruence of 2-D Shapes
Definition:
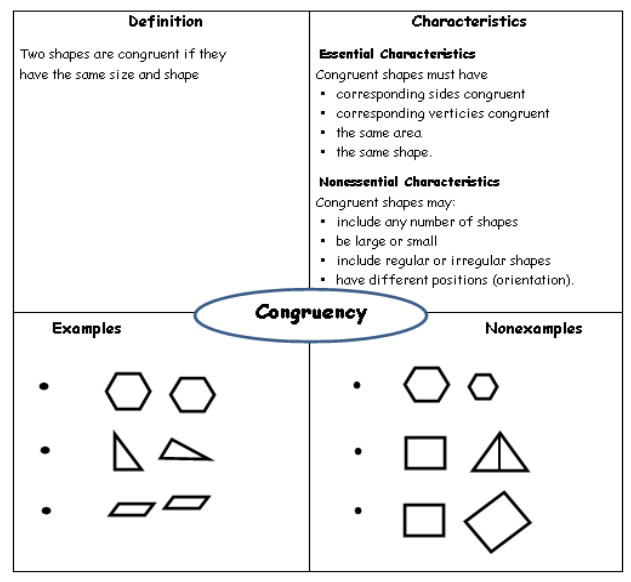
Two 2-D shapes are congruent if they are identical in shape and size.
It is important to recognize that the term congruent applies only to size and shape. The figures can be different colors, or oriented in different ways, and they will still be congruent as long as they are the same shape and the same size.
Characteristics:
Congruent shapes must have
• corresponding sides congruent
• corresponding vertices congruent
• the same area
• the same shape
The following Frayer Model gives a summary of congruency for 2-D shapes.
Congruent - Grade 4 Common Core Standards
This video examine the meaning of congruence.
Example:
Denise drew the figure below.
Which figure is congruent to the figure Denise draw?
Symmetry of 2-D Shapes
Definition:
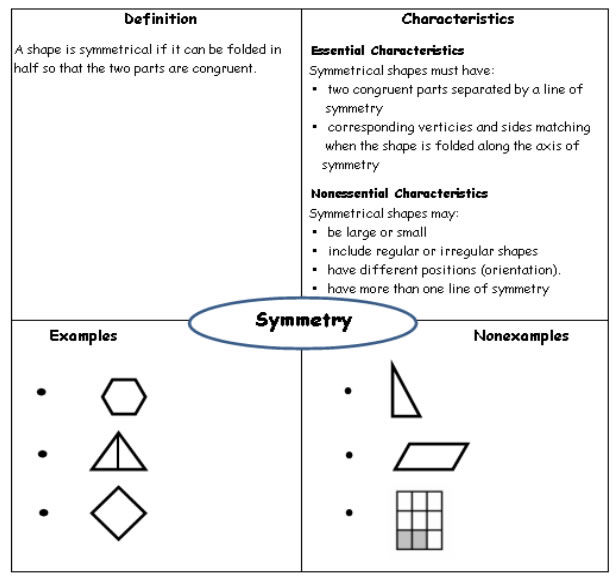
A 2-D figure has line symmetry when it can be divided or folded so that the two parts match exactly.
The fold line is called the line of symmetry. Any given line of symmetry divides a figure into equal halves. It may also be said that each of the halves are mirror images of each other.
Line symmetry is also called reflective symmetry or mirror symmetry.
Characteristics:
Symmetrical shapes must have:
• two congruent parts separated by a line of symmetry
• corresponding vertices and sides matching when the shape is folded along the axis of symmetry
The following Frayer Model gives a summary of symmetry for 2-D shapes.
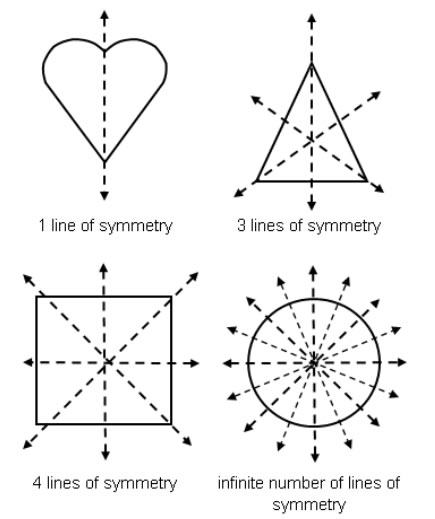
Shapes may have multiple lines of symmetry and the lines of symmetry can be vertical, horizontal, or diagonal. The more sides that a regular polygon has, the greater the number of lines of symmetry there are. A circle has an infinite number of lines of symmetry.
Lines of symmetry - Grade 3 Common Core Standards
In this video, we find lines of symmetry in a 2D shape.
Example:
Which figure shows a line of symmetry?
Multiple Lines of Symmetry
Looking at a few problems with more than one line of reflective symmetry.
Line Symmetry
This video will review with you the basics of line symmetry and how to find line symmetry.
A figure has line symmetry if a line can be drawn through the figure so that each half is a mirror image of the other.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.