

Central Angles and Congruent Arcs
Related Topics:
More Lessons for Grade 9
Math Worksheets
Examples, solutions, videos, worksheets, and activities to help Geometry students learn about central angles and arcs.
The measure of a central angle is equal to the measure of its intercepted arc.
The following diagram shows that the angle measure of the central angle is equal to the measure of the intercepted arc. Scroll down the page for more examples and solutions.
Central angle is an angle whose vertex is on the center of the circle and whose endpoints are on the circle. The endpoints on the circle are also the endpoints for the angle's intercepted arc. The angle measure of the central angle is congruent to the measure of the intercepted arc which is an important fact when finding missing arcs or central angles.
Circle Geometry: Identifying Congruent Central Angles, Chords, and Arcs
This geometry video math lesson deals with circle geometry. It focuses on how to identify congruent central angles, chords, and arcs when given either a central angle, a chord, or an arc.
In the same circle, or congruent circles, congruent central angles have congruent arcs.
In the same circle, or congruent circles, congruent arcs have congruent central angles
In the same circle, or congruent circles, congruent central angles have congruent chords.
In the same circle, or congruent circles, congruent chords have congruent central angles.
Central Angles and Intercepted Arcs
Central angles and arc measures (Semicircles or Half Circles)



More Lessons for Grade 9
Math Worksheets
Examples, solutions, videos, worksheets, and activities to help Geometry students learn about central angles and arcs.
The measure of a central angle is equal to the measure of its intercepted arc.
The following diagram shows that the angle measure of the central angle is equal to the measure of the intercepted arc. Scroll down the page for more examples and solutions.
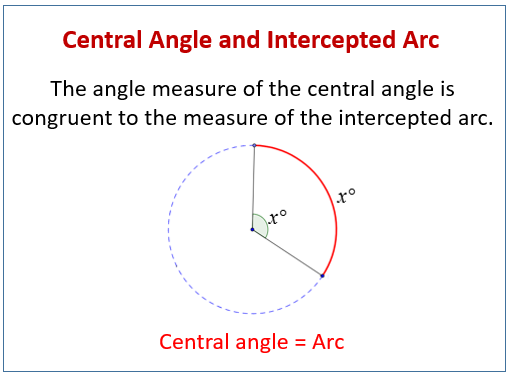
Central angle is an angle whose vertex is on the center of the circle and whose endpoints are on the circle. The endpoints on the circle are also the endpoints for the angle's intercepted arc. The angle measure of the central angle is congruent to the measure of the intercepted arc which is an important fact when finding missing arcs or central angles.
This geometry video math lesson deals with circle geometry. It focuses on how to identify congruent central angles, chords, and arcs when given either a central angle, a chord, or an arc.
In the same circle, or congruent circles, congruent central angles have congruent arcs.
In the same circle, or congruent circles, congruent arcs have congruent central angles
In the same circle, or congruent circles, congruent central angles have congruent chords.
In the same circle, or congruent circles, congruent chords have congruent central angles.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.