Complement Of A Set
Related Pages
Venn Diagrams
Union Of Sets
Intersection Of Two Sets
More Lessons on Sets
This page is part of a series of lessons on sets.
In these lessons, we will learn the complement of a set and the relative complement of a set.
The following diagram shows the complement of a set. Scroll down the page for more examples and solutions on the complement of a set.
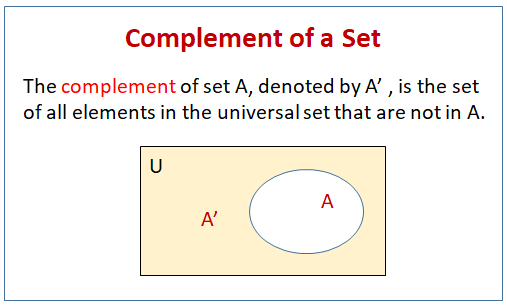
The complement of set A, denoted by A’ , is the set of all elements in the universal set that are not in A.
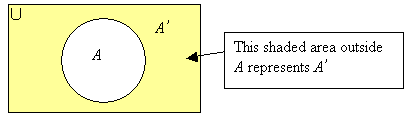
The number of elements of A and the number of elements of A ’ make up the total number of elements in U .
n(A) + n(A’) = n(U)
Example:
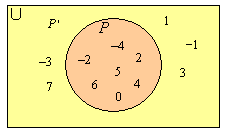
Let U = {x : x is an integer, –4 ≤ x ≤ 7}, P = {–4, –2, 0, 2, 4, 5, 6} and
Q ’ = {–3, –2, –1, 2, 3}.
a) List the elements of set P ’
b) Draw a Venn diagram to display the sets U , P and P ’
c) Find n(Q)
Solution:
a) First, list out the members of U.
U = {–4, –3, –2, –1, 0, 1, 2, 3, 4, 5, 6, 7}
P ’ = {–3, –1, 1, 3, 7} ← in U but not in P
b) Draw a Venn diagram to display the sets U , P and P ’
c) Find n(Q)
n( U ) = 12, n(Q ’ ) = 5
Use the formula:
n(Q) + n(Q ’ ) = n( U )
n(Q) = n( U ) – n(Q ’ ) = 12 – 5 = 7
Set Worksheets
Subsets
Distinguish between subsets and proper subsets. Find the number of subsets in a given set.
Complement of a Set
Universal set, complement of a set, and subsets.
Complement and Relative Complement
The complement of a set is the collection of all elements which are not members of that set. Although this operation appears to be straightforward, the way we define “all elements” can significantly change the results.
Learn what a complement of a set is
Universal set and absolute complement
Relative complement or difference between sets
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.