From Circle-ometry to Trigonometry

From Circle-ometry to Trigonometry

Student Outcomes

• Students will define sine and cosine as functions for degrees of rotation of the ray formed by the positive -axis up to one full turn.
• Students use special triangles to geometrically determine the values of sine and cosine for 30, 45, 60, and 90 degrees.

New York State Common Core Math Algebra II, Module 2, Lesson 4

Worksheets for Algebra 2

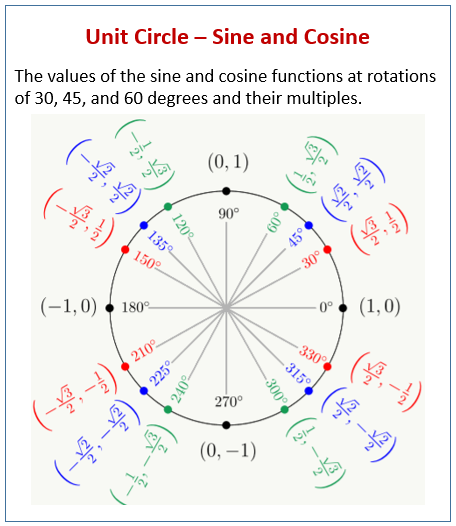
The values of the sine and cosine functions at rotations of 30, 45, and 60 degrees and multiples of these rotations come up often in trigonometry. The diagram below summarizes the coordinates of these commonly referenced points.

 

Classwork

Opening Exercises

1. Find the lengths of the sides of the right triangles below, each of which has hypotenuse of length 1.
2. Given the following right triangle △ 𝐴𝐵𝐶 with 𝑚∠𝐴 = 𝜃°, find sin(𝜃°) and cos(𝜃°).

• Show Video for Whole Lesson

Example 1 Suppose that point 𝑃 is the point on the unit circle obtained by rotating the initial ray through 30°. Find sin(30°) and cos(30°).
What is the length 𝑂𝑄 of the horizontal leg of our triangle?
What is the length 𝑄𝑃 of the vertical leg of our triangle?
What is sin(30°)?
What is cos(30°)?

Exercises 1–2

1. Suppose that 𝑃 is the point on the unit circle obtained by rotating the initial ray through 45°. Find sin(45°) and cos(45°).
2. Suppose that 𝑃 is the point on the unit circle obtained by rotating the initial ray through 60°. Find sin(60°) and cos(60°).

Example 2
Suppose that 𝑃 is the point on the unit circle obtained by rotating the initial ray through 150°. Find sin(150°) and cos(150°).

Exercises 3–5
3. Suppose that 𝑃 is the point on the unit circle obtained by rotating the initial ray counterclockwise through 120 degrees. Find the measure of the reference angle for 120°, and then find sin(120°) and cos(120°). 4. Suppose that 𝑃 is the point on the unit circle obtained by rotating the initial ray counterclockwise through 240°. Find the measure of the reference angle for 240°, and then find sin(240°) and cos(240°). 5. Suppose that 𝑃 is the point on the unit circle obtained by rotating the initial ray counterclockwise through 330 degrees. Find the measure of the reference angle for 330°, and then find sin(330°) and cos(330°).

Lesson Summary
In this lesson we formalized the idea of the height and co-height of a Ferris wheel and defined the sine and cosine functions that give the 𝑥- and 𝑦- coordinates of the intersection of the unit circle and the initial ray rotated through 𝜃 degrees, for most values of 𝜃 with 0 < 𝜃 < 360.

• The value of cos(𝜃°) is the 𝑥-coordinate of the intersection point of the terminal ray and the unit circle.
• The value of sin(𝜃°) is the 𝑦-coordinate of the intersection point of the terminal ray and the unit circle.
• The sine and cosine functions have domain of all real numbers and range [−1,1]

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.