Circle Theorem Examples
In this lesson, we will learn
- a Circle Theorem called the “Thales’ Theorem” or “Triangle inscribed in semicircle” or “Angle inscribed in semicircle” or “90 degrees in Semicircle” Theorem.
- how to use the Thales’ Theorem to find missing angles.
- how to prove the Thales’ Theorem.
Thales’ theorem
The Thales’ theorem states
Every angle subtended at the circumference by the diameter of a circle is a right angle (90˚).
or
The diameter of a circle always subtends a right angle to any point on the circle.
or
The angle inscribed in a semicircle is 90˚.
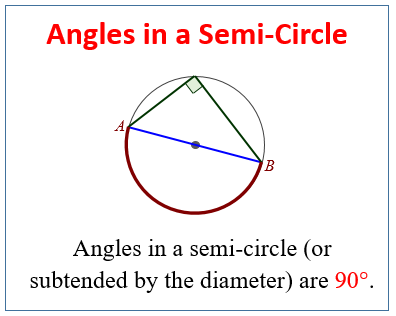
The following diagram shows the Thales’ Theorem: Angles in a semi-circle are 90°. Scroll down the page for more examples and solutions.
Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets
Using the Theorem
Example:
O is the centre of the circle. Find the value of x

Solution:
∠ABC = 90˚ ( angle in a semicircle = 90˚)
63˚ + 90˚ + x = 180˚ ( sum of angles in a triangle )
x = 27˚
Inscribed Right Triangles (Right Triangles Inside of Circles)
Thales’ Theorem: If the longest side of a triangle inscribed within a circle is the same length as the diameter of a circle, then that triangle is a right triangle, as well as the converse: if a right triangle is inscribed within a circle, the length of its hypotenuse is the diameter of the circle.
We can use the Thales’ Theorem to find missing angles.
Proving the Theorem
Proof of the Thales’ Theorem
Proof showing that a triangle inscribed in a circle having a diameter as one side is a right triangle.
This proof uses the bow theorem.
Converse of Thales’s Theorem
The converse of Thales’s Theorem is also true:
If a right triangle is inscribed in a circle, then its hypotenuse is a diameter of the circle.
Practical Applications
A. Finding Right Angles
Example: A semicircular arch guarantees a right angle at its apex.
B. Construction
Ancient Egyptians used Thales’ theorem to build perfect right angles for pyramids.
C. Coordinate Geometry
If points A, B, and C lie on a circle with BC as the diameter, then vectors BA and CA are perpendicular.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.