Angles Of Elevation And Depression
Related Pages
Angles
Trigonometry
More Geometry Lessons
In these lessons, we will study some practical applications of trigonometry in the calculation of angles of elevation and angles of depression.
Angles of elevation and depression are fundamental concepts in trigonometry, often used in real-world applications to calculate heights, distances, and depths. They are always measured between a horizontal line and the line of sight.
What Is Angle Of Elevation?
The angle of elevation is the angle between a horizontal line from the observer and the line of sight to an object that is above the horizontal line.
In the diagram below, AB is the horizontal line. θ is the angle of elevation from the observer at A to the object at C.
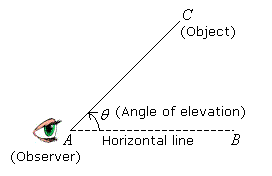
The angle of elevation is the angle formed when an observer looks up at an object.
Observer’s Position: Below the object.
Line of Sight: Goes upwards from the observer’s eye to the object.
Horizontal Line: A theoretical line extending straight out from the observer’s eye level, parallel to the ground.
The Angle: The angle is formed above the horizontal line.
What Is Angle Of Depression?
The angle of depression is the angle between a horizontal line from the observer and the line of sight to an object that is below the horizontal line.
In the diagram below, PQ is the horizontal line. θ is the angle of depression from the observer at P to the object at R.
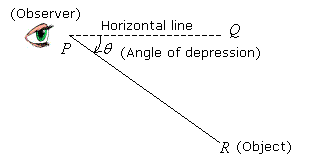
The angle of depression is the angle formed when an observer looks down at an object.
Observer’s Position: Above the object.
Line of Sight: Goes downwards from the observer’s eye to the object.
Horizontal Line: A theoretical line extending straight out from the observer’s eye level, parallel to the ground.
The Angle: The angle is formed below the horizontal line.
Videos
How To Define An Angle Of Elevation Or An Angle Of Depression?
Find angles of depression and angles of elevation, and the relationship between them.
Angles of elevation and depression are equal.
Example:
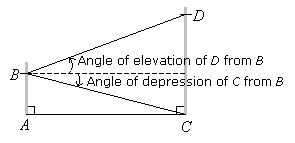
In the diagram below, AB and CD are two vertical poles on horizontal ground. Draw in the angle
of elevation of D from B and the angle of depression of C from B.

Solution:
How To Solve Word Problems That Involve Angle Of Elevation Or Depression?
Step 1: Draw a sketch of the situation.
Step 2: Mark in the given angle of elevation or depression.
Step 3: Use trigonometry to find the required missing length.
Example:
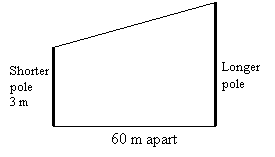
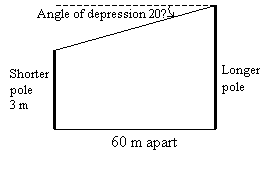
Two poles on horizontal ground are 60 m apart. The shorter pole is 3 m high. The angle of
depression of the top of the shorter pole from the top of the longer pole is 20˚. Sketch
a diagram to represent the situation.
Solution:
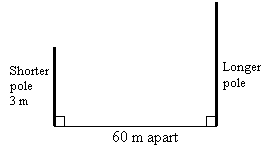
Step 1: Draw two vertical lines to represent the shorter pole and the longer pole.
Step 2: Draw a line from the top of the longer pole to the top of the shorter pole. (This is the line of sight).
Step 3: Draw a horizontal line to the top of the pole and mark in the angle of depression.
Example:
A man who is 2 m tall stands on horizontal ground 30 m from a tree. The angle of elevation of the top of
the tree from his eyes is 28˚. Estimate the height of the tree.
Solution:
Let the height of the tree be h. Sketch a diagram to represent the situation.
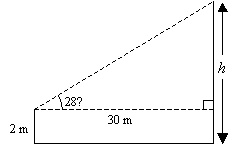
tan 28˚ = ![]()
h – 2 = 30 tan 28˚
h = (30 ´ 0.5317) + 2 ← tan 28˚ = 0.5317
h = 17.95
The height of the tree is approximately 18.0 m. (rounded)
How To Solve Word Problems Involving Angles Of Elevation And Angles Of Depression?
Examples:
- An observer standing on top of a vertical spots a house in the adjacent valley at an angle of depression of 12°. The cliff is 60m tall. How far is the house from the base of the cliff?
- Buildings A and B are across the street from each other, 35m apart. From a point on the roof of Building A the angle of elevation at the top of Building B is 24°, and the angle of depression of the base of Building B is 34°. How tall is each building?
How To Solve Word Problems Using Tangent And The Angle Of Depression?
Applications of Trig Functions: Solving for unknown distances.
Example:
How far away is a boat from the lighthouse if the lighthouse is 120° tall and the angle
of depression to boat is 15°?
How To Solve Word Problems Using Tangent And The Angle Of Elevation?
Example:
A boat is 500 meters from the base of a cliff. Jackie, who is sitting in the boat, notices that
the angle of elevation to the top of the cliff is 32°15’. How high is the cliff? (Give your
answer to the nearest meter).
Angle Of Elevation And Depression Word Problems
Examples:
- From a boat on the lake, the angle of elevation to the top of the cliff is 24°22’. If the base of the cliff is 747 feet from the boat, how high is the cliff (to the nearest foot)?
- From a boat on the river below a dam, the angle of elevation to the top of the dam is 24° 8’. If the dam is 2039 feet above the level of the river, how far is the boat from the base of the dam (to the nearest foot)?
- If a man is just about to ski down a steep mountain. He estimates the angle of depression from where he is now to the flag at the bottom of the course to be 24°. He knows that he is 800 feet higher than the base of the course. How long is the path that he will ski? (Round to the nearest foot)
- a) A man at ground level measures the angle of elevation to the top of the building to be
67°. If at this point, he is 15 feet away from the building, what is the height of the
building?
b) The same man now stands atop a building. He measures the angle of elevation to the building across the street to be 27° and the angle of depression (to the base of the building across the street) to be 31°. If the two buildings are 50 feet apart, how tall is the taller building?
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.