Alternate Interior Angles & Alternate External Angles
Related Pages
Corresponding Angles
Co-Interior Angles
Interior Angles of a Triangle
Geometry Help
In these lesson, we will learn the properties of alternate interior angles and alternate exterior angles.
In geometry, pairs of angles can relate to each other in several ways. Here we shall look at
- alternate interior angles
- proof of the alternate interior angle theorem
- proof of the converse of the alternate interior angle theorem
- alternate exterior angles
- proof of the alternate exterior angle theorem
- proof of the converse of the alternate exterior angle theorem
Alternate Interior Angles and Alternate Exterior Angles
The following figure shows some examples of alternate interior and alternate exteriors angle pairs. Scroll down the page if you need more examples and explanations about alternate interior angles and alternate exterior angles.
-
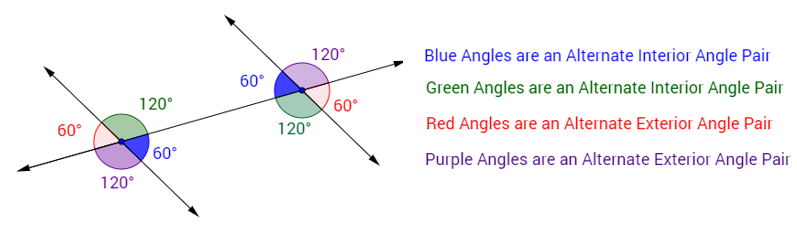
Printable & Online Angle Worksheets
Printable
Types of Angles (Acute, Obtuse, Right)
Angles on a Straight Line
Vertical Angles
Complementary Angles
Supplementary Angles
Complementary & Supplementary Angles
Angles at a Point
Calculate Adjacent AnglesOnline
Types of Angles
Angles in a Straight Line
Angles at a Point
Complementary Angles
Supplementary Angles
Alternate Interior Angles
When a line (called a transversal) intersects a pair of lines, alternate interior angles are formed on opposite sides of the transversal. If the pair of lines are parallel then the alternate interior angles are equal to each other.
The Alternate Interior Angles Theorem states that
When two parallel lines are cut by a transversal, the resulting alternate interior angles are congruent.
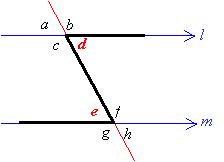
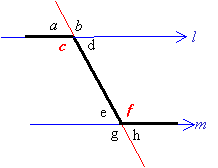
How to identify Alternate Interior Angles?
One way to find the alternate interior angles is to draw a zig-zag line on the diagram. In the above diagrams, d and e are alternate interior angles. Similarly, c and f are also alternate interior angles.
(Angles found in a Z-shaped figure)
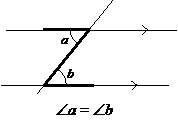
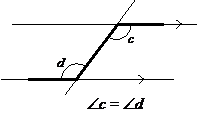
How to use the Alternate Angle Theorem to find missing angles?
Example 1:
Given the diagram below, determine the values of the angles b,
c, d, e, f, g and h.
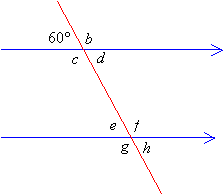
Solution:
Step 1: b is a supplement of 60°
Therefore, b + 60° = 180° ⇒ b = 180° 60° = 120°
Step 2: b and c are vertical angles.
Therefore, c = b = 120°
Step 3: d and 60° are vertical angles.
Therefore, d = 60°
Step 4: d and e are alternate interior angles.
Therefore, e = d = 60°
Step 5: f and e are supplementary angles.
Therefore, f + 60° =180° ⇒ f = 180° 60° = 120°
Step 6: g and f are vertical angles.
Therefore, g = f = 120°
Step 7: h and e are vertical angles.
Therefore, h = e = 60°
Answer: b = 120° c = 120°, d = 60° e = 60° f = 120° g = 120° and h = 60°
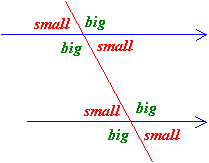
From the above example, you may notice that either an angle is 60° or it is 120° Actually, all the small angles are 60° and all the big angles are 120°
In general, the diagram will be as shown below. The small and big pair of angles are supplementary (i.e. small + big = 180°. Therefore, given any one angle you would be able to work out the values of all the other angles.
How to identify alternate interior angles and their properties?
A transversal is a line that passes through two lines. Alternate interior angles are angles that are on the inside of the two lines, and on the opposite sides of the transversal. If the two lines are parallel then the alternate interior angles are congruent.
If lines are parallel then corresponding angles are congruent, alternate interior angles are congruent and alternate exterior angles are congruent.
If lines are parallel, then same side interior angles are supplementary and same side exterior angles are supplementary.
How to solve for x using Alternate Interior Angles?
How to use alternate interior angles to find the measures of angles?
Proof of the Alternate Interior Angle Theorem
This video will prove that Alternate Interior Angles are congruent by using the Corresponding Angle Postulate.
How to prove the Alternate Interior Angle theorem showing that when lines are parallel, alternate interior angles are congruent?
What is the Converse of the Alternate Interior Angles Theorem?
The Converse of the Alternate Interior Angle Theorem states that
If two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.
How to prove of the Converse of the Alternate Interior Angles Theorem?
This video shows a proof of the alternate interior angle converse.
Alternate Exterior Angles
When two lines are crossed by a transversal, the opposite angle pairs on the outside of the lines are alternate exterior angles. If the two lines are parallel then the alternate exterior angles are congruent.
One way to identify alternate exterior angles is to see that they are the vertical angles of the alternate interior angles. Alternate exterior angles are equal to one another.
The Alternate Exterior Angles Theorem states that
When two parallel lines are cut by a transversal, the resulting alternate exterior angles are congruent.
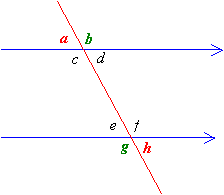
a and h are alternate exterior angles and they are equal to one another.
b and g are alternate exterior angles and they are equal to one another.
Alternate Exterior Angles definition and properties
This video shows how to identify alternate exterior angles and their properties.
When two lines are crossed by a transversal, the opposite angle pairs on the outside of the lines are alternate exterior angles. If the two lines are parallel then the alternate exterior angles are congruent.
Find out how to locate alternate exterior angles and the characteristics of alternate exterior angles.
How to find an angle using alternate exterior angle?
Proof of the Alternate Exterior Angle
Proof and definition of alternate and exterior angles with a transversal and parallel lines.
Proof of the Alternate Exterior Angle Converse
The Converse of the Alternate Exterior Angle Theorem states that
If two lines are cut by a transversal and the alternate angles are congruent, then the lines are parallel.
This video shows a proof of the alternate exterior angle converse.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.