Factors And Multiples
Factors And Multiples
If a is divisible by b, then b is a factor of a, and a is a multiple of b. For example, 30 = 3 × 10, so 3 and 10 are factors of 30 and 30 is a multiple of 3 and 10
Take note that 1 is a factor of every number.
Understanding factors and multiples is essential for solving many math problems.
Prime Factors
A factor which is a prime number is called a prime factor. For example, the prime factorization of 180 is 2 × 2 × 3 × 3 × 5
You can use repeated division by prime numbers to obtain the prime factors of a given number.
The following diagram shows how to find the GCF using the Ladder Method. Scroll down the page for more examples and solutions.
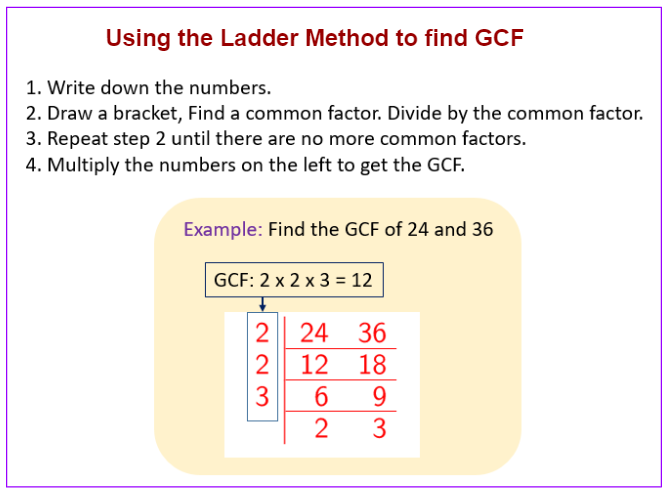
Greatest Common Factor (GCF)
As the name implies, we need to list the factors and find the greatest one that is common to all the numbers. For example, to get the GCF of 24, 60 and 66:
The factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24 The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60
The factors of 66 are 1, 2, 3, 6, 11, 22,33 and 66
Look for the greatest factor that is common to all three numbers - thus 6 is the GCF of 24, 60 and 66.
Least Common Multiple (LCM)
As the name implies, we need to list the multiples and to find the least one that is common to all the numbers. For example, to get the LCM of 3, 6 and 9:
The multiples of 3 are 3, 6, 9, 12, 15, 18, 21 … The multiples of 6 are 6, 12, 18, 24, …
The multiples of 9 are 9, 18, 27, …
Look for the least multiple that is common to all three numbers - thus 18 is the LCM of 3, 6 and 9.
Shortcut To Finding LCM
Here is a useful shortcut (also called the ladder method) to finding the LCM of a set of numbers. For example, to find the LCM of 3, 6 and 9, we divide them by any factor of the numbers in the following manner:
How to use the Ladder method to find GCF, LCM and simplifying fractions?
Step 1: Write the two numbers on one line.
Step 2: Draw the L shape.
Step 3: Divide out common prime numbers starting with the smallest.
LCM makes an L.
GCF is down the left side.
Simplified fraction is on the bottom.
Example:
Find the GCF, LCM and simplified fraction for 24 and 36.
LCM & GCF With the Ladder Method
Example:
Find the LCM and GCF of 24 and 36.
Difference between greatest common factor and least common multiple
Example: Find the GCF and LCM of 16 and 24.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.