Algebra: Age Problems

Solving Age Problems in Algebra

If the problem involves a single person, then it is similar to an Integer Problem. Read the problem carefully to determine the relationship between the numbers. See example involving a single person.

In this lesson, we will learn how to solve age problems that involve the ages of two or more people.

Solving age word problems involving two or more people can seem complex, but using a table to organize the information makes it much easier. This is shown in the following age word problems that involve more than one person.

Age Problems Involving More Than One Person

The following diagram shows how to solve an age word problem involving three people. Scroll down the page for more examples and solutions.

 

Algebra Worksheets
Practice your skills with the following Algebra worksheets:
Printable & Online Algebra Worksheets

How to use a table to solve Age Word Problems

1. Identify the People and Time Frames
   List the people involved and the time frames.
   
2. Create a Table
   
3. Fill in Known Values
   Assign a variable (e.g., x) to the unknown present age.
   Express other ages in terms of x.
   
4. Set Up the Equation
   Use the given relationship (sum, difference, ratio) to form an equation.
   
5. Solve for x and Find All Ages

Here are some common types of Age Word Problems

Example:
John is twice as old as his friend Peter. Peter is 5 years older than Alice. In 5 years, John will be three times as old as Alice. How old is Peter now?

Solution:
Step 1: Set up a table.

 

Step 2: Fill in the table with information given in the question.
John is twice as old as his friend Peter. Peter is 5 years older than Alice. In 5 years, John will be three times as old as Alice. How old is Peter now?

Let x be Peter’s age now. Add 5 to get the ages in 5 yrs.

 

Write the new relationship in an equation using the ages in 5 yrs.

In 5 years, John will be three times as old as Alice.
2x + 5 = 3(x – 5 + 5)
2x + 5 = 3x

Isolate variable x
x = 5
Answer: Peter is now 5 years old.

Example:
John’s father is 5 times older than John and John is twice as old as his sister Alice. In two years time, the sum of their ages will be 58. How old is John now?

Solution:
Step 1: Set up a table.

 

Step 2: Fill in the table with information given in the question.
John’s father is 5 times older than John and John is twice as old as his sister Alice. In two years time, the sum of their ages will be 58. How old is John now?

Let x be John’s age now. Add 2 to get the ages in 2 yrs.

 

Write the new relationship in an equation using the ages in 2 yrs.

In two years time, the sum of their ages will be 58.

 

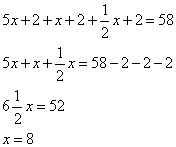
Answer: John is now 8 years old.

Video Lessons - More Examples Age Word Problems

Example:
Mary is 3 times as old as her son. In 12 years, Mary’s age will be one year less than twice her son’s age. Find their ages now.

Note that this problem requires a chart to organize the information. The rows of the chart can be labeled as Mary and Son, and the columns of the chart can be labeled as “age now” and “age in 12 years”. The chart is then used to set up the equation.

• Show Video Lesson

Examples:

1. Sue is 5 years younger than Brian. In 7 years, the sum of their ages will be 49 years. How old is each now?
2. Maria is 10 years older than Sonia. Eight years ago, Maria was 3 times Sonia’s age. How old is each now?

• Show Video Lesson

Examples:

1. The sum of the ages of a man and his son is 82 years. How old is each, if 11 years ago, the man was twice his son’s age?
2. The sum of the ages of a woman and her daughter is 38 years. How old is each, if the woman will be triple her daughter’s age in 9 years?

• Show Video Lesson

Examples:

1. Salman is 108 years old. Jonathan is 24 years old. How many years will it take for Salman to be exactly four times as old as Jonathan?
2. Tarush is five times as old as Arman is today. 85 years ago, Tarush was 10 times as old as Arman. How old is Arman today?

• Show Video Lesson

Example: Zack is four times as old as Salman. Zack is also three years older than Salman. How old is Zack?

• Show Video Lesson

Examples For Practise:

1. Soo is 8 years older than Marco. In four years, Soo will be twice as old as Marco. How old is Soo?
2. The sum of Abbie’s age and Iris’s age is 42 years old. 11 years ago, Abbie was three times as old as Iris. How old will Abbie be in two years?

Check out many other Algebra Word Problems
Age Word Problems, Average Word Problems, Coin Word Problems, Consecutive Integer Word Problems, Digit Word Problems, Distance Word Problems, Fraction Word Problems, Geometry Word Problems, Integer Word Problems, Interest Word Problems, Lever Word Problems, Mixture Word Problems, Money Word Problems, Motion & Distance Word Problems, Number Sequence Word Problems, Proportion Word Problems, Quadratic Equation Word Problems, Ratio Word Problems, Symbol Word Problems, Variation Word Problems, Work Word Problems.

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.