30-60-90 Special Right Triangles

30-60-90 Triangles

A 30-60-90 triangle is a special type of right triangle where the angles are 30°, 60°, and 90°. The sides of a 30-60-90 triangle follow a consistent ratio of 1:√3:2 making calculations quick and easy. If we are given one side of the triangle, we are able to easily find the other sides using the ratio of 1:√3:2.

Another special right triangle is the 45-45-90 triangle.

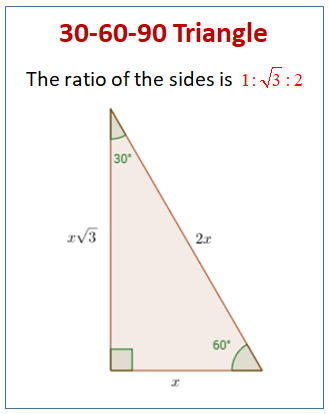
The following diagram shows the properties of a 30-60-90 Triangle. Scroll down the page for more examples and solutions on how to solve 30-60-90 Triangles.

Geometry Worksheets
Practice your skills with the following geometry worksheets:
Printable & Online Geometry Worksheets

Side Length Ratio: 1:√3:2
Shortest side (opposite 30°) = x
Middle side (opposite 60°) = x√3
Hypotenuse (opposite 90°) = 2x

How to Use 30-60-90 Triangles
If you know the length of just one side of a 30-60-90 triangle, you can find the lengths of the other two sides using these ratios.
Case 1: Given the shortest side (x)
Hypotenuse = 2x
Medium side = x√3
Example: If the side opposite the 30° angle is 7, then the hypotenuse is 2×7=14, and the side opposite the 60° angle is 7√3.

Case 2: Given the hypotenuse (2x)
Shortest side = x
Medium side = x√3
Example: If the hypotenuse is 10, then the side opposite the 30° angle = 10/2 = 5 and the side opposite the 60° angle is 5√3.

Case 3: Given the medium side (x√3)
Shortest side = x
Hypotenuse = 2x
Example: If the side opposite the 60° angle is 6√3, then the side opposite the 30° angle is 6. The hypotenuse is 2×6=12.

Importance

• Efficiency: It allows you to solve for unknown side lengths much faster than using the Pythagorean theorem or trigonometric functions (sine, cosine, tangent) for every problem.
• Exact Values: It provides exact radical answers, which are often preferred over decimal approximations.
• Trigonometry: The side ratios are the basis for exact trigonometric values for 30° and 60° (e.g., sin(30°)=1/2, cos(60°)=1/2, tan(30°)=1/3).
• Problem Solving: It’s frequently encountered in standardized tests and real-world problems involving geometry and right triangles.

How to find the legs and hypotenuse in 30-60-90 triangles when given: the short leg, the long leg, or the hypotenuse.

• Show Video Lesson

Solve a 30-60-90 Right Triangle
This video provides examples of how to solve a 30-60-90 triangle given the length of one side.

• Show Video Lesson

30-60-90 Triangle

• Show Video Lesson

Finding the Missing Side of 30-60-90 Triangle

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.