Volume of a Rectangular Prism
In these lessons, we will learn
- how to find the volume of a rectangular prism.
- how to solve word problems about rectangular prisms.
Related Pages
Volume Formulas
Volume Of Pyramids
Explanations For The Surface Area Formulas
More Geometry Lessons
Solid geometry is concerned with three-dimensional shapes.
Volume of a Rectangular Prism
A rectangular prism is a 3-dimensional object with six rectangular faces. All its angles are right angles and opposite faces are equal.
In a rectangular prism, the length, width and height may be of different lengths. A rectangular prism is also called a cuboid or rectangular solid. A cube is a special case of a cuboid in which all six faces are squares.
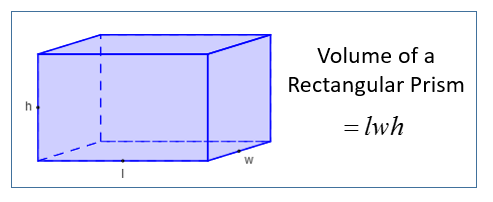
The volume of the above rectangular prism would be the product of the length, width and height that is
Volume of rectangular prism = lwh
Surface area of rectangular prism = 2(lw + wh + lh)
Worksheet to calculate the volume and surface area of a rectangular prism.
Example:
Find the volume of the following rectangular prism or cuboid.

Solution:
Volume = l × w × h
= 6 cm × 3 cm × 4 cm
= 72 cm3
Reviews the concept of volume and uses a rectangular prism as an example
How to find the volume of two rectangular prisms?
Word problems about rectangular prisms
The following video shows how to solve a word problem involving a rectangular prism.
Example:
An exotic fish is placed in a rectangular aquarium that has a length of 75 cm and a width of 35 cm.
If the water level rises 2 cm when the fish is placed in the aquarium, what is the volume of the fish?
Volume and Surface Area of a Rectangular Solid
How to solve problems for volume of a rectangular prism?
Example:
If 1 cubic centimetre = 1 ml of water, how much water can fit in this fish tank?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.