Volume of Cylinders

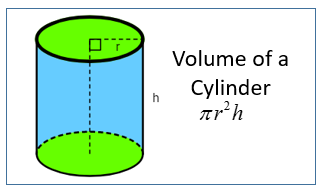
Volume of a Cylinder
The volume of a cylinder is the amount of three-dimensional space it occupies. A cylinder is a solid geometric shape with two parallel and congruent circular bases connected by a curved surface.

Formula for the Volume of a Cylinder

The following diagram gives the formula for volume of a cylinder. Scroll down the page for more examples and solutions on how to use the volume of cylinder formula.

Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets

The formula for the volume (V) of a cylinder is:
V = πr²h

Where:
V = Volume of the cylinder
π (pi) is a mathematical constant, approximately 3.14159.
r = radius of the circular base of the cylinder.
h = height of the cylinder (the perpendicular distance between the two circular bases)

Explanation of the Formula Components
πr²: This part of the formula represents the area of the circular base of the cylinder. You’ll recognize this as the formula for the area of a circle.
h: This is the height of the cylinder.
Essentially, the formula calculates the area of the circular base and then multiply by the height of the cylinder to get its volume.

How to find the Volume of Solid Cylinders?

Example:
Calculate the volume of a cylinder where:
a) the area of the base is 30 cm ² and the height is 6 cm.
b) the radius of the base is 14 cm and the height is 10 cm.

Solution:
a) V = Area of base × height
= 30 cm² × 6 am
= 180 cm³

b)

How to find the volume of a cylinder?
Examples:

1. Find the volume of cylinder with radius of 5.5 feet and a height of 11.4 feet.
   
2. Find the volume of cylinder with diameter of 12 inches and a height of 29 inches.

• Show Step-by-step Solutions

How to find the volume of a right cylinder?
Example:
Find the volume with r = 9 in and h = 12 in. (Leave your answer in &oi; form)

• Show Step-by-step Solutions

How to find the volume of Hollow Cylinders?
Sometimes you may be required to calculate the volume of a hollow cylinder or tube or pipe.

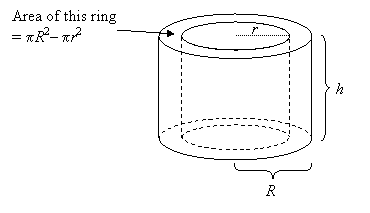
To find the volume of a hollow cylinder, you calculate the volume of the larger, outer cylinder and then subtract the volume of the smaller, inner cylinder (the empty space).

Volume of hollow cylinder:
= πR² h – πr² h
= πh (R²– r²)

Important Note: Make sure you are using radii, not diameters. If you are given diameters, divide them by 2 to get the radii.

Example:
The figure shows a section of a metal pipe. Given the internal radius of the pipe is 2 cm, the external radius is 2.4 cm and the length of the pipe is 10 cm. Find the volume of the metal used.

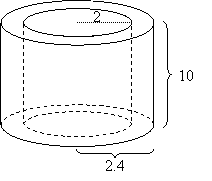
Solution:
The cross section of the pipe is a ring:
Area of ring = π(2.4)² – π(2)² = 1.76π cm²
Volume of pipe = 1.76 π × 10 = 55.3 cm³
Volume of metal used = 55.3 cm³

How to find the volume of a cylinder in a prism?
Examples:
A cylindrical can is packed securely in a box.
a) Find the radius and height of the can.
b) What is the volume of the empty space between the can and the box?
c) Find the ratio of the volume of the can to the volume of the box.

• Show Step-by-step Solutions

How to solve word problems about cylinders?
These videos show how to solve word problems about cylinders.
Examples:

1. A cylindrical can is packed in a box. What is the volume of empty space between the can and the box?
   
2. Emma has two prism-shaped containers. One has a volume of 9 1/3 cubic feet. How many smaller prisms would it take to fill the larger prism?
   

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.