Transformation Of Trigonometric Graphs
Related Pages
Lessons On Trigonometry
Trigonometric Functions
Stretching And Compressing of Graphs
Transformations of Trigonometric Graphs
In these lessons, we will learn
- how Trigonometric Graphs can be transformed
- the amplitude and vertical shift of Trigonometric Graphs
- the period and phase shift of Trigonometric Graphs
Transformations of trigonometric graphs involve altering the basic shape of the parent functions (like y=sinx, y=cosx, and y=tanx) by stretching, compressing, shifting, or reflecting them. Understanding these transformations is key to graphing trigonometric functions.
The following diagrams show how to determine the transformation of a Trigonometric Graph from its equation. Scroll down the page for more examples and solutions.
Trigonometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Trigonometry Worksheets
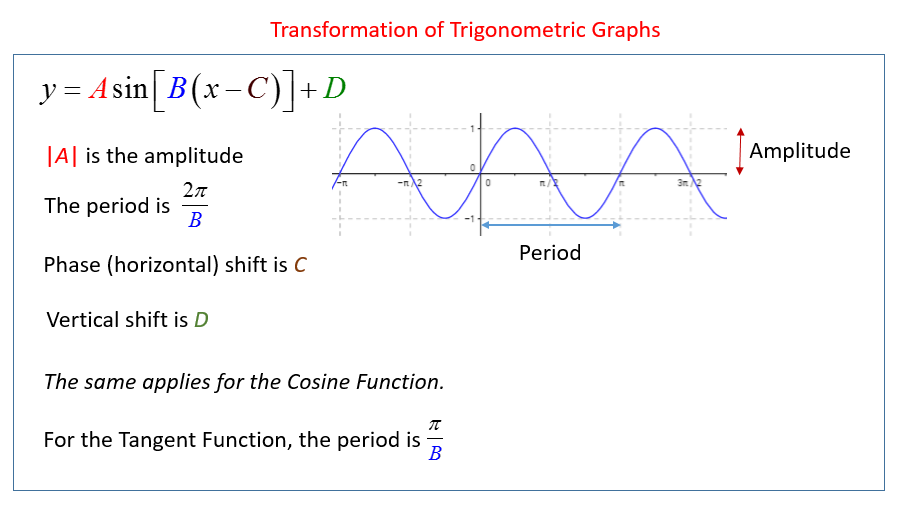
The general form of a transformed sinusoidal (sine or cosine) function is often written as:
y = A sin(B(x−C)) + D or y = A cos(B(x−C)) + D
Amplitude Of Trigonometric Functions (A)
The amplitude of a trigonometric function is the maximum displacement on the graph of that function.
In the case of sin and cos functions, this value is the leading coefficient of the function.
If y = A sin x or y = A cos x, then the amplitude is |A|.
If |A| > 1, the graph is vertically stretched (taller waves).
If 0 < |A| < 1, the graph is vertically compressed (shorter waves)
In the case of tan, cot, sec, and csc, the amplitude would be infinitely large regardless of the value of A. However, for a limited domain, the value of A would determine the maximum height of these functions.
Period of Trigonometric Function (B)
The period of a function is the displacement of x at which the graph of the function begins to repeat.
Consider y = sin x

The value x = 2π is the point at which the graph begins to repeat that of the first quadrant. The coefficient of x is the constant that determine the period.
The general form is y = A sin Bx where |A| is the amplitude and B determines the period.
For the functions sin, cos, sec and csc, the period is found by \(P = \frac{2π}{B}\)
Example:
Find the period of the graph y = sin 2x and sketch the graph of y = sin 2x for 0 ≤ 2x ≤ π.
Solution:
Since B = 2, the period is \(P = \frac{2π}{B}= \frac{2π}{2} = π\)

Phase Shift of Trigonometric Functions (C)
The general form for the equation of the sine trigonometric function is
y = A sin B(x + C)
where A is the amplitude, the period is calculated by the constant B, and C is the phase shift.
The graph y = sin x may be moved or shifted to the left or to the right. If C is positive, the shift is to the left; if C is negative the shift is to the right.
A similar general form can be obtained for the other trigonometric functions.
Example:
Find the amplitude, period and phase shift of
\(y=2\text{sin}\left( 2x+\frac{\pi}{2} \right)\)
Solution:
Rewrite as
\(y=2\text{sin}2\left( x+\frac{\pi}{4} \right)\)
The amplitude is 2, the period is π and the phase shift is \(\frac{π}{4}\) units to the left.
Vertical Shift (D)
The general form for the equation of the sine trigonometric function is
y = A sin B(x + C) + D
where A is the amplitude, the period is calculated by the constant B, C is the phase shift, and D is the vertical shift.
The parameter D controls the vertical shift (translation) of the entire graph. It determines the position of the midline of the wave.
The midline of the graph is the horizontal line y = D. If D > 0, the graph shifts upward. If D < 0, the graph shifts downward.
Videos
Basic Sine Function
Periodic Functions Definition, Period, Phase Shift, Amplitude, Vertical Shift.
A periodic function is a function whose graph repeats itself identically from left to right.
The period of a function is the horizontal distance required for a complete cycle.
The period of a basic sine and cosine function is 2π.
The frequency of a function is the reciprocal of the period.
The phase shift of a function is the horizontal shift of a periodic function.
The amplitude of a function is half the distance between the maximum and minimum values of a periodic function. The amplitude is always positive.
The vertical shift of a function is the vertical shift of a periodic function along the y-axis.
Transformation of sin and cos with amplitude and vertical shift
f(x) = A sin (Bx + C) + D
Expand vertically when |A| > 1
Contract vertically when |A| < 1
Reflect when A < 1
Amplitude = |A|
Transformation of sin and cos with period and phase shift
f(x) = A sin (Bx + C) + D
Contract horizontally when |B| > 1
Expand horizontally when 0 < |B| < 1
Period = (2π)/|B|
Examples of transforming basic sine and cosine functions
f(x) = A sin (Bx + C) + D
Shift up vertically when D > 0
Shift down vertically when D < 0
Demonstrations of Transformations of Trigonometric Graphs: Amplitude, Period & Phase Shift
Graph trig functions (sine, cosine, and tangent) with all of the transformations
The videos explained how to the amplitude and period changes and what numbers in the equations.
Part 1: See what a vertical translation, horizontal translation, and a reflection behaves in three separate examples.
Example 1: Sketch the graph of y = 3 + sin 2x
Example 2: Sketch the graph of y = -1 + cos(x - π)
Graph trig functions (sine, cosine, and tangent) with all of the transformations
In this set of videos, we see how the line of equilibrium is affected by a vertical shift, and how the
starting point is affected by a horizontal shift (phase). Shifts of graphs up and down are also called translations.
Part 2: An example of how the tangent graph and its asymptotes are affected different transformations.
An example that includes every kind of transformation possible, all in one problem, is shown.
Example 1: Sketch the graph of y = -3 tan x + 5
Example 2: Sketch the graph y = 2 + 3 cos 4π (x + 1/4)
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.