Translation Transformation
Related Pages
Transformations In Math
Geometric Transformations
Transformations In The Coordinate Plane
Rotation
More Geometry Lessons
In these lessons, we will learn
- what is translation
- how translation can be represented by a column matrix or column vector
- how to translate points and shapes on the coordinate plane
What Is Translation?
In a translation transformation all the points in the object are moved in a straight line in the same direction. The size, the shape and the orientation of the image are the same as that of the original object. Same orientation means that the object and image are facing the same direction.
Example:
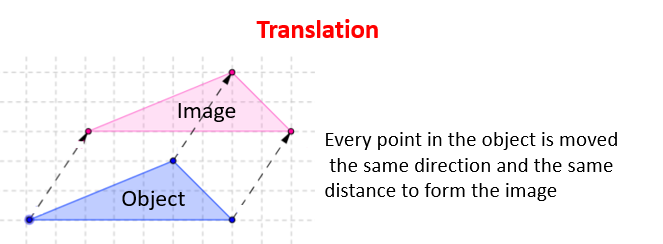
We describe a translation in terms of the number of units moved to the right or left and the number of units moved up or down.
Example:
Move the object 2 units to the right and 4 units up.
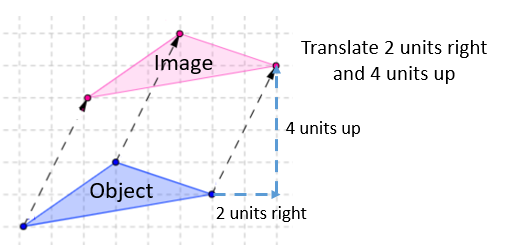
Translation Represented By Column Vector Or Matrix
The translation can be represented by a column vector as
.
The top number represents the right and left movement. A positive number means moving to the right and a negative number means moving to the left.
The bottom number represents up and down movement. A positive number means moving up and a negative number means moving down.
In the following figure, triangle ABC is being translated to triangle A’B’C’
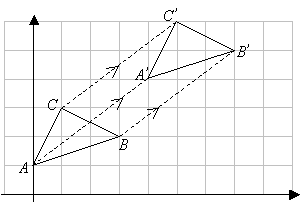
The translation is represented by the column vector
.
In general, a translation can be represented by a column matrix or column vector
where
a is the number of units to move right or left along the x-axis and b is the number of units to
move up or down along the y-axis.
The matrix equation representing a translation is:
where
is the translation matrix and 
is the image of 
.
Example 1:
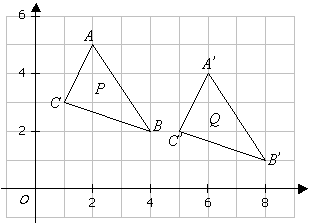
The triangle P is mapped onto the triangle Q by the translation 
.
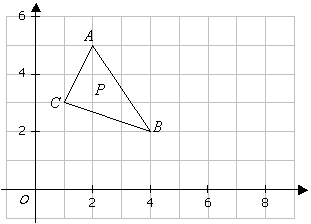
a) Find the coordinates of triangle Q.
b) On the diagram, draw and label triangle Q.
Solution:
a)
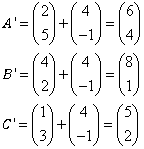
b)
As a mathematical notation, we may write: T(A) = B, to mean object A is mapped onto B under the transformation T.
Describing translations of simple shapes in the plane, using column vector notation
How to transform a shape using a given vector?
Translation On The Coordinate Plane
Geometry Translation
A geometry translation is an isometric transformation, meaning that the original figure and
the image are congruent. Translating a figure can be thought of as “sliding” the original.
If the image moved left and down, the rule will be (x - __, y - __) where the blanks are the
distances moved along each axis; for translations left and up: (x - __, y + __), for right
and down (x + __, y - __), for right and up (x + __, y + __).
How to translate a polygon on the coordinate plane?
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.