Slicing 3 D Shapes
These lessons, with videos, examples, solutions and worksheets help Grade 7 students learn how to describe the two-dimensional figures that result from slicing three-dimensional figures, as in plane sections of right rectangular prisms and right rectangular pyramids.
Related Pages
Cross Section of 3D objects (worksheets)
Common Core for Grade 7
More Math Lessons for Grade 7
Common Core for Mathematics
More Geometry Lessons
Common Core: 7.G.3
Suggested Learning Targets
- I can describe two dimensional figures that result from slicing three-dimensional figures (by a plane parallel or perpendicular to a base or face).
What is a cross section?
A cross section is the two-dimensional shape that results from cutting a three-dimensional
shape with a plane. The shape of the cross section depends on the type of “cut”
(vertical, angled, horizontal).
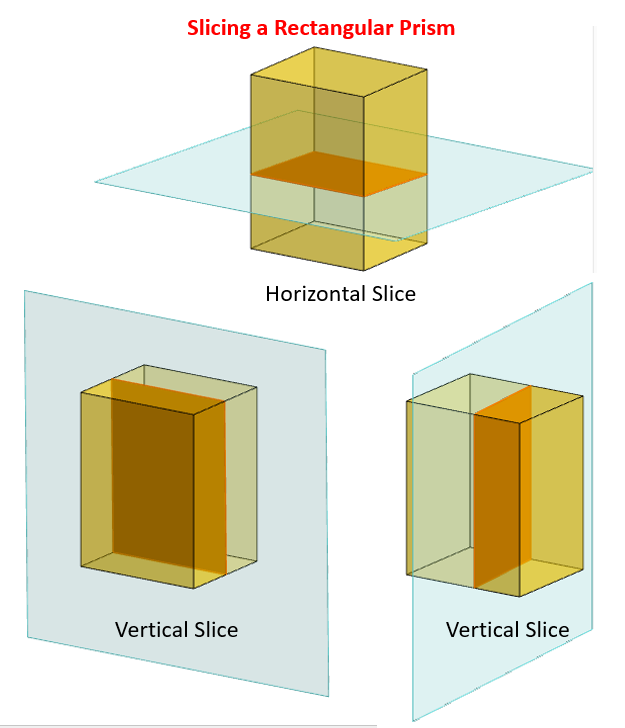
The following diagrams show the horizontal and vertical slices of a rectangular prism. Scroll down the page for examples and solutions.
How to describe the cross sections of a right rectangular prism by slicing at different angles?
Describe the two-dimensional figures that result from slicing three-dimensional figures (7.G.3)
Example:
A chef needs a piece of cheese for a new recipe. The chef makes a straight top
to bottom slice from a block of cheese.
How are the attributes of the piece of cheese and the attributes of the block of
cheese alike? How are they different? Explain your reasoning.
A cross section is the intersection of a three-dimensional figure and a plane. You can think of a cross section as a two-dimensional slice of the figure.
A vertical slice can be parallel to the left and right faces. The cross section always has the same shape and dimensions as there faces.
A vertical slice can also be parallel to the front and back faces. The cross section always has the same shape and dimensions as these faces.
A horizontal slice is parallel to the bases. The cross section always has the same shape and dimensions as these faces.
How to draw cross sections?
Examples:
- Given all prisms below are the same dimensions, draw the cross section that would be formed from the “slice” shown.
- Draw and describe a cross section formed by a plane that slices a cube as follows.
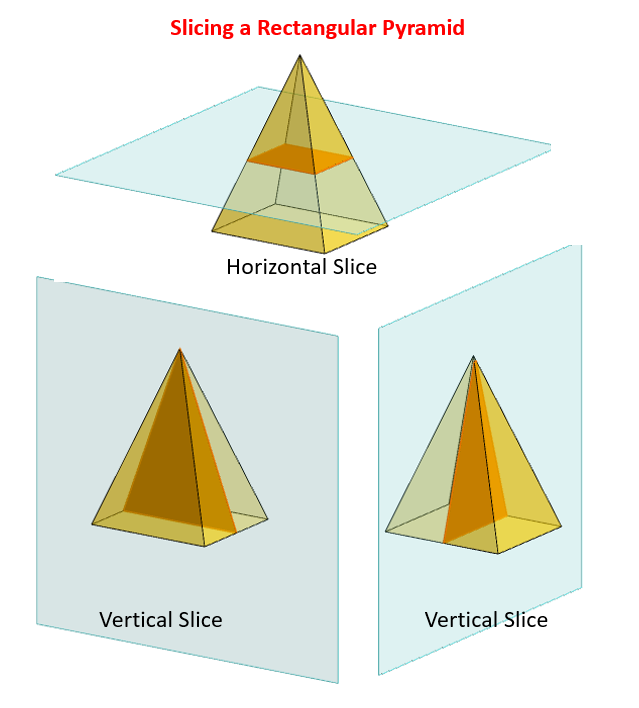
The following diagrams show the horizontal and vertical slices of a rectangular pyramid. Scroll down the page for examples and solutions.
How to describe the cross sections of a right rectangular pyramid by slicing at different angles?
Example:
A waiter slices his restaurant’s world-famous meatloaf as shown for two diners to share.
Could the waiter’s split be even? Is there a better way to make sure? Explain.
If you make any horizontal slice of a rectangular pyramid, the resulting cross section, or slice, is a rectangle. The size of the rectangle depends on the distance of the slice from the base.
If you make a vertical slice of a rectangular pyramid through the vertex, the resulting cross
section, or slice, is an isosceles triangle. The base of the triangle is equal in length to an
edge of the triangular base. The height of the triangle is equal to the height of the pyramid.
Examples:
- Draw the shape and label dimensions for the cross section formed.
- What are the shape and dimensions of the cross section formed by slicing the pyramid as shown?
- Explain how to slice a rectangular pyramid to get an isosceles trapezoid cross section?
- Draw and describe a cross section formed by a plane that slices a rectangular pyramid as follows.
a. The plane is vertical and intersects the front face and the vertex of the pyramid.
b. The plane is horizontal and halfway up the pyramid. - Draw and describe two triangular cross sections, each formed by a plane that intersects the vertex and is perpendicular to the base.
- Explain how to slice a rectangular pyramid through the vertex to get triangles of many different heights.
Nets and Cross Sections of Solids
A cross section is the intersection of a solid and a plane.
Example:
Draw the cross section created when a vertical plane intersects the right and the front
faces of the polyhedron.
Slicing 3-D Figures
A cross section is the two-dimensional shape that results from cutting a three-dimensional with a plane.
How to identify the face shape from cuts made parallel and perpendicular to the bases of right
dimensional figures?
Parallel cuts will take the shape of the base.
Perpendicular cuts will take the shape of the lateral face.
Cuts made at an angle through the right rectangular prism or pyramid will produce a parallelogram.
Cross Sections of 3 Dimensional Figures
A cross section is the intersection of a solid (3-dimensional object) and a plane figure
(2-dimensional object). The shape of the cross section depends on the type of cut that happens
to the figure (vertical, angled, or horizontal)
Example:
The fruit to the right has been slice horizontally. Since the fruit represented is usually
a sphere, the resulting cross section is a circle.
Horizontal slice, vertical slice and angled slice of a rectangular pyramid.
Horizontal slice, vertical slice and angled slice of a cylinder.
What is the shape of the cross section?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.