Similar Triangles
Related Pages
Similar Triangles: Angle-Angle Criterion
Congruent Triangles
Geometry Lessons
In these lessons, we will learn
- the properties of similar triangles,
- how to tell if two triangles are similar using the similar triangle theorem: AA rule, SAS rule or SSS rule,
- how to solve problems using similar triangles.
Properties Of Similar Triangles
Similar triangles have the following properties:
- They have the same shape but not the same size.
- Each corresponding pair of angles is equal.
- The ratio of any pair of corresponding sides is the same.
The following diagrams show similar triangles. Scroll down the page for more examples and solutions on how to detect similar triangles and how to use similar triangles to solve problems.
Printable & Online Geometry Worksheets
If triangles are similar then the ratios of the corresponding sides are equal.
When the ratio is 1 then the similar triangles become congruent triangles (same shape and size).
How To Tell If Two Triangles Are Similar?
We can tell whether two triangles are similar without testing all the sides and all the angles of the two triangles. There are three rules or theorems to check for similar triangles.
As long as one of the rules is true, it is sufficient to prove that the two triangles are similar.
Two triangles are similar if any of the following is true.
-
AA (Angle-Angle)
The two angles of one triangle are equal to the two angles of the other triangle. (AA rule) -
SAS (Side-Angle-Side)
Two sides are in the same proportion, and their included angle is equal. (SAS rule) -
SSS (Side-Side-Side)
The three sides are in the same proportion. (SSS rule).
Scroll down the page for more examples and solutions on the AA Rule, SAS rule, SSS rule and how to solve problems using similar triangles.
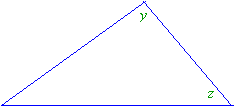
AA Rule
The Angle-Angle (AA) rule states that
If two angles of one triangle are equal
to two angles of another triangle, then the triangles are similar.
 |
 |
This is also sometimes called the AAA rule because equality of two corresponding pairs of angles would imply that the third corresponding pair of angles are also equal.
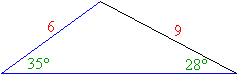
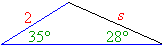
Example 1:
Given the following triangles, find the length of s
 |
 |
Solution:
Step 1: The triangles are similar because of the AA rule.
Step 2: The ratios of the lengths are equal.
Step 3: Cross multiplying: 6s = 18 ⇒ s = 3
Answer: The length of s is 3.
SAS Rule
The Side-Angle-Side (SAS) rule states that
If the angle of one triangle is the same
as the angle of another triangle and the sides containing these
angles are in the same ratio, then the triangles are similar.
 |
 |
Example 2:
Given the following triangles, find the length of s
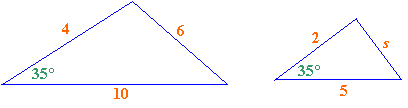
Solution:
Step 1: The triangles are similar because of the RAR rule.
Step 2: The ratios of the lengths are equal.
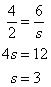
Answer: The length of s is 3.
SSS Rule
The Side-Side-Side (SSS) rule states that
If two triangles have their corresponding sides in the same ratio,
then they are similar.
How to solve similar triangles using AA, SAS, and SSS?
The following video shows the AA, SAS and SSS similarity theorem and how to use them.
You can show that two triangles are similar when you know the relationships between only two or three pairs of the corresponding parts.
Angle-Angle Similarity (AA) Postulate: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.
Side-Angle-Side Similarity (SAS) Theorem: If an angle of one triangle is congruent to an angle of a second triangle, and the sides that include the two angles are proportional, then the triangles are similar.
Side-Side-Side Similarity (SSS) Theorem: If the corresponding sides of two triangles are proportional, then the triangles are similar.
Examples:
- Are the following triangle similar? How do you know?
- Are the triangles similar? If so, write a similarity statement for the triangles?
Sometimes you can use similar triangle to find lengths that cannot be measured easily using a ruler or other measuring device. You can use indirect measurement to find lengths that are difficult to measure directly. One method of indirect measurement uses the fact that light reflects off a mirror at the same angle at which it hits the mirror.
Example:
Before rock climbing, Darius wants to know how high he will climb. He places a mirror on the
ground and walks backward until he can see the top of the cliff in the mirror. What is the
height of the cliff?
How to determine whether two triangles are similar using AA similarity?
The Third Angle Theorem states that if two angles in one triangle are congruent to two
angles in another triangle, the third angle must be congruent also.
The AA Similarity Postulate: If two angles in one triangle are congruent to two angles in another triangle, then the triangles are similar.
Example:
Determine if the following triangles are similar.
How to determine whether two triangles are similar using SSS and SAS similarity?
If the corresponding sides of two triangles are proportional, then the two triangles are similar.
If the two sides of two triangles are proportional and the included angles are congruent, the the triangles are similar.
Example:
Determine if the following triangles are similar.
How to solve for unknown values using the properties of similar triangles?
Example:
Given that the triangles are similar, determine x and y.
How to find the length of a side of a triangle using similar triangles (Overlapping)?
Indirect Measurement Using Similar Triangles
How to use the properties of similar triangles to determine the height of a tree?
An application of similar triangles is to be able to determine lengths indirectly. Remember the sides of similar triangles are proportional.
Examples of how to solve problems using similar triangles
Example 1: Fred needs to know how wide a river is. He takes measurements as shown in the diagram.
Determine the river’s width.
Example 2: Determine the ratio of the areas of the two similar triangles.
Example 3: If the area of the smaller triangle is 20 m2, determine the area of the larger triangle.
How to use similar triangles to solve shadow problems?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.