Rotational Symmetry
Related Pages
Lines Of Symmetry
Polygons & Symmetry
More Geometry Lessons
These lessons help Geometry students learn about rotational symmetry, with video lessons, examples and solutions.
In these lessons, we will learn
- what is rotational symmetry?
- how to find the order of rotation.
- how to find the angle of rotation.
What Is Rotational Symmetry?
Symmetry in a figure exists if there is a reflection, rotation, or translation that can be performed and the image is identical.
Rotational symmetry is a type of symmetry a shape has when it looks exactly the same after being rotated by a certain angle around a central point. Imagine spinning the shape around its center; if it perfectly matches its original appearance before completing a full 360-degree turn, it has rotational symmetry.
A regular polygon has a degree of rotational symmetry equal to its number of sides.
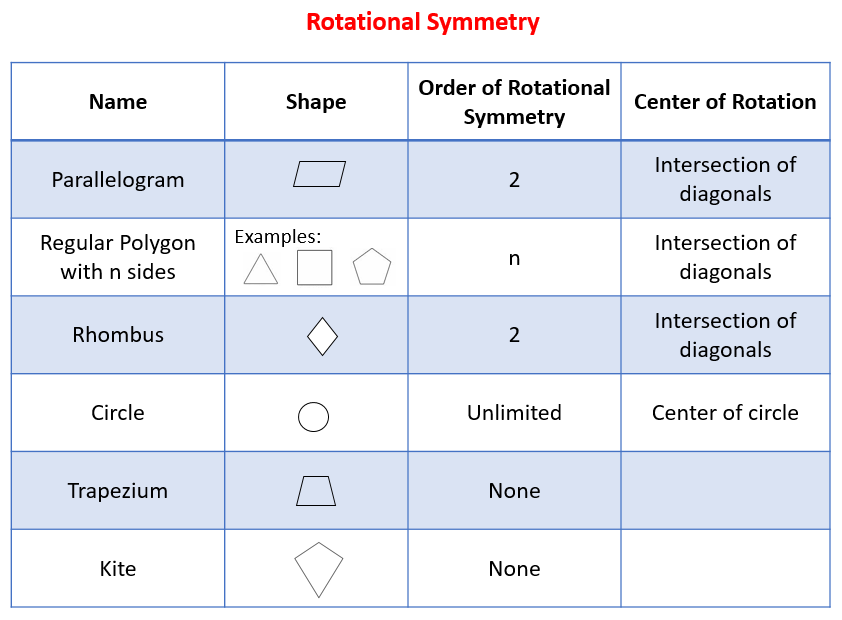
The following table gives the order of rotational symmetry for parallelogram, regular polygon, rhombus, circle, trapezium, kite. Scroll down the page for examples and solutions.
Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets
What Is The Order Of Rotation And Angle Of Rotation?
The Center of Rotation is the fixed point around which the shape rotates. For regular polygons and many symmetric objects, this is typically the geometric center of the shape.
The Angle of Rotational Symmetry is the smallest angle (greater than 0° and less than 360°) through which a shape can be rotated to look exactly like its original self.
The Order of Rotational Symmetry refers to the number of times a shape looks identical to its original position during one full 360-degree rotation. It includes the original position itself as one count.
The angle of rotation for a regular figure is 360 degrees divided by the order of rotational symmetry.
How To Find The Order Of Rotational Symmetry Of A Shape?
The order of rotational symmetry is the number of times you can rotate a shape so that it looks the same. The original position is counted only once (i.e. not when it returns to its original position)
The order of rotational symmetry of a regular polygon is the same as the number of sides of the polygon.
You can also deduce the order of rotational symmetry by knowing the smallest angle you can
rotate the shape through to look the same.
180° = order 2,
120° = order 3,
90° = order 4.
The product of the angle and the order would be 360°.
How to relate between a reflection and a rotation and examine rotational symmetry within an individual figure
The following video will give the solutions for the Rotations, Reflections and Symmetry Worksheet. (NYS Common Core, Geometry Lesson Module 1, Lesson 15)
Opening Exercise
The original triangle, labeled A, has been reflected across the first line, resulting in the
image labeled B. Reflect the image across the second line. Carlos looked at the image of the
reflection across the second line and said, “That’s not the image of triangle A after two
reflections; that’s the image of triangle A after a rotation!” Do you agree? Why or why not?
Discussion
When you reflect a figure across a line, the original figure and its image share a line of
symmetry, which we have called the line of reflection. When you reflect a figure across a
line and then reflect the image across a line that intersects the first line, your final
image is a rotation of the original figure. The center of rotation is the point at which
the two lines of reflection intersect. The angle of rotation is determined by connecting
the center of rotation to a pair of corresponding vertices on the original figure and the
final image. The figure above is a 210° rotation (or 150° clockwise rotation).
Exploratory Challenge
Line of symmetry of a figure: This is an isosceles triangle. By definition, an isosceles
triangle has at least two congruent sides. A line of symmetry of the triangle can be drawn
from the top vertex to the midpoint of the base, decomposing the original triangle into two
congruent right triangles. This line of symmetry can be thought of as a reflection across
itself that takes the isosceles triangle to itself. Every point of the triangle on one side
of the line of symmetry has a corresponding point on the triangle on the other side of the
line of symmetry, given by reflecting the point across the line. In particular, the line of
symmetry is equidistant from all corresponding pairs of points. Another way of thinking about
line symmetry is that a figure has line symmetry if there exists a line (or lines) such that
the image of the figure when reflected over the line is itself.
Does every figure have a line of symmetry?
How to find the angle of rotation for regular polygons?
The angle of rotation of a regular polygon is equal to 360° divided by the number of sides.
Rotational Symmetry
The order of Rotational Symmetry tells us how many times a shape looks the same when it rotate 360 degrees. Determine the order of rotational symmetry for a square, a rectangle and an equilateral triangle.
Basic Rotational Symmetry
Introduction to rotational symmetry with fun shapes.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.