Rotation Transformation
Related Pages
Transformations In Math
Geometric Transformations
Transformations In The Coordinate Plane
Translation
More Geometry Lessons
In these lessons, we will learn
- what is rotation Click here
- how to draw the rotated image of an object given the center, the angle & the direction of rotation. Click here
- how to find the angle of rotation given the object, its image & the center of rotation. Click here
- how to rotate points & shapes on the coordinate plane about the origin. Click here
- examples of composition of transformations. Click here
What Is Rotation?
A rotation is a transformation in which the object is rotated about a fixed point.
The direction of rotation can be clockwise or anticlockwise.
The fixed point in which the rotation takes place is called the center of rotation. The amount of rotation made is called the angle of rotation.
Example:
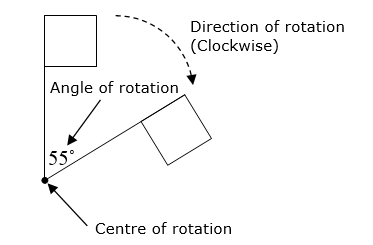
For any rotation, we need to specify the center, the angle and the direction of rotation.
Drawing The Rotated Image
Given the center of rotation and the angle of rotation we can determine the rotated image of an object.
Example:
Determine the image of the straight line XY under an anticlockwise rotation of 90˚ about O.
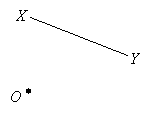
Solution:
Step 1: Join point X to O.
Step 2: Using a protractor, draw a line 90˚ anticlockwise from the line OX. Mark on the line the point X’ such that the line of OX’ = OX
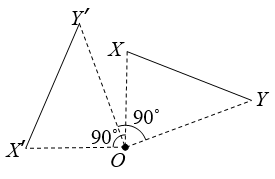
Step 3: Repeat steps 1 and 2 for point Y. Join the points X’ and Y’ to form the line X’Y’.
The Angle Of Rotation
Given an object, its image and the center of rotation, we can find the angle of rotation using the following steps.
Step 1: Choose any point in the given figure and join the chosen point to the center of rotation.
Step 2: Find the image of the chosen point and join it to the center of rotation.
Step 3: Measure the angle between the two lines. The sign of the angle depends on the direction of rotation. Anti-clockwise rotation is positive and clockwise rotation is negative.
Example:
Figure A’B’C’ is the image of figure ABC. O is the center of rotation.
Find the angle of rotation.
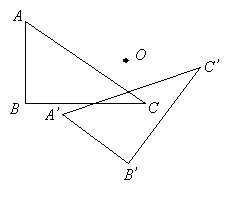
Solution:
Step 1: Join A to O.
Step 2: Join A’ to O.
Step 3: Measure the angle AOA’.

The angle of rotation is 62˚ anticlockwise or +62˚
Manual rotation of a polygon about a given point at a given angle
You will need a straightedge, a protractor, and a compass. We will perform rotations about a point inside the figure, one outside the figure and one on the figure.
Examples:
- Rotate ABCD by 143° about point P.
- Rotate JKLM by 111° about point Q.
How to rotate a figure around a fixed point using a compass and protractor?
You are given:
- A center of rotation.
- A figure to rotate.
- An angle of rotation.
- Draw a ray from the center of rotation to the point you wish to rotate.
- Draw an angle with the center of rotation as the vertex.
- Use a compass to draw a circle (arc) with the center at the center of rotation and a radius from the center of rotation to the point you are rotating.
- Now rotate all the other points and connect the dots.
Rotate Points On The Coordinate Plane
We will now look at how points and shapes are rotated on the coordinate plane. It will be helpful to note the patterns of the coordinates when the points are rotated about the origin at different angles.
A rotation is an isometric transformation: the original figure and the image are congruent. The orientation of the image also stays the same, unlike reflections. To perform a geometry rotation, we first need to know the point of rotation, the angle of rotation, and a direction (either clockwise or counterclockwise). A rotation is also the same as a composition of reflections over intersecting lines.
The following diagrams show rotation of 90°, 180° and 270° about the origin. Scroll down the page for more examples and solutions.
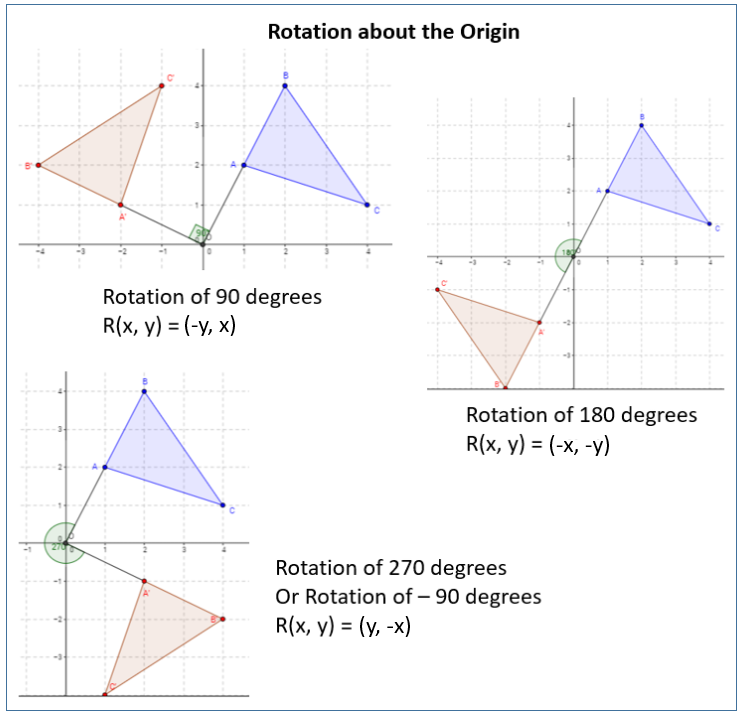
Coordinate Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Coordinate Geometry Worksheets
How to rotate points on the coordinate plane?
The following videos show clockwise and anticlockwise rotation of 0˚, 90˚, 180˚ and 270˚about the origin (0, 0). The pattern of the coordinates are also explored.
Composition Of Transformations
Reflection in intersecting lines Theorem
If lines k and m intersect at a point P, then a reflection in k followed by a reflection in m is
the same as a rotation about point P.
The angle of rotation is 2x° where x° is the measure of the acute angle formed by the lines k and m.
Two reflections in parallel lines = translation.
Two reflections in intersecting lines = rotation.
Example:
Below is a composition of two reflection in intersecting lines. What is a single transformation that
would map ABCD onto A"B"C"D"?
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.