

Ratio and Proportion - GRE
More Lessons for GRE Math
Math Worksheets
This lesson is part of a series of lessons for the quantitative reasoning section of the GRE revised General Test. In this lesson, we will learn:
- Ratios
- Proportions
Ratio
A ratio is a comparison between two quantities in the form of a quotient.
The ratio of A and B can be written in 3 ways: • A to B• A:B
• A/B
For example:
There are 3 red sweets and 5 yellow sweets in the box. We can say the ratio of red sweets to yellow sweets is 3 to 5. Ratio can be written with the symbol ':' or as a fraction.
'3 to 5' can be written as '3:5' or ![]()
Like fractions, ratios can be reduced to lowest terms.
For example, if there are 6 red sweets and 10
yellow sweets in the box, then the ratio of the numbers of red sweets to yellow sweets is 6:10 which can be reduced to 3:5.
A three-term ratio can be used to compare three quantities, for example:
There are 5 red sweets, 15 yellow sweets and 30 blue sweets in
the box
5 to 15 to 30 = 5:15:30 which can be reduced (divide by 5) to 1:3:6
Examples:
1. A class has 15 female students and 12 male students.
a) What is the ration of males to females?
b) What is the ratio of females to males?
c) What is the ratio of females to total students?
2. The team played a total of 24 games last season. They won 18 games and lost 6 games.
a) What is the ratio of wins and losses?
b) What is the ratio of wins to total games?
What is the ratio of losses to total games?
Write a Ratio as a Simplified Fractions Involving Decimals and Fractions
Examples:
2/9 to 7/18
0.06 to 0.24
Proportion
A proportion is an equation relating two ratios.
For example, ![]()
To solve a problem involving ratios, you can often write a proportion and solve it by cross multiplication.
Example:
If two pens cost $1.50, how many pens can you buy with $9.00?
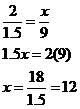
You can buy 12 pens
Example:
If the ratio of the number of men to the number of women on a committee of 20 members is 3 to 2, how many members of the committee are women?
men : women : total = 3 : 2 : 5
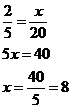
There are 8 women in the committee.
How to solve proportion problems using the cross product method?A proportion states that two ratios or rates are equal.
If a/b and c/d are two equal ratios, then a/b = c/d is a proportion.
a/b = c/d if and only if a • d = b • c
If two fractions are equal, then the cross products are equal.
If the cross products are equal, then the fractions are equal.
Examples:
Write ratios for the pairs of numbers and then determine if they form a proportion.
1. 24, 36 and 1.8, 2.7
2. 10, 8 and 14, 11
Steps to solve for a missing number in a proportion.
1. Find the cross products and form an equation.
2. Solve the equation.
3. Check your answer.
Example:
Solve
a) 8/2.4 = 18/n
b) y/1 = 6/5
Applications of Proportions
Example:
1. The directions on the label of an over the counter fever reducer states to take 10 milligrams of liquid per 40 lbs of body weight every 6 hours. If you weigh 140 lbs, how much medicine should you take?
2. A team of forest rangers need to estimate the population of deer on government land. They catch 100 deer and tag and release them. Later, they catch 40 deer and 8 of them have tags. Estimate the deer population.
3. You plan to drive from Phoenix, AZ to Houston, TX which is 1175 miles. If you travel 442 miles in 2 days, how many total days will the drive take?
4. The sides of similar triangles are proportional. Determine the length of the missing side.
5. A yard stick casts a shadow that is 2 feet long. If te shadow of flagpole is 25 feet long, how tall is the flagpole?
How to solve a proportion word problem?
Example:
Arthur is typing a paper that is 390 words long. He can type 30 words in 1 minute. How long will it take him to type the paper?
How to solve word problems by writing and solving a proportion?
Example:
A recipe has 5 cups of flour for every 2 cups of sugar. If I want to make a recipe with 8 cups of flour, how much sugar should I use?
Example:
On a map two cities are 2 5.8 inches apart. If 3/8 inches on the map represent 25 miles, how far apart are the cities in miles?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.