Degrees and Radians
In this lesson, we will learn
- how to measure angles in degrees, minutes and seconds
- how to convert an angle measured in degrees, minutes and seconds to decimal notation and vice versa.
- how to add and subtract angles measured in degrees, minutes and seconds
- how to measure angles in radians
- how to convert between degree and radian measurement
The following diagrams show how to define radian in terms of the arc length and the radius and how to convert between radians and degrees. Scroll down the page for examples and solutions.
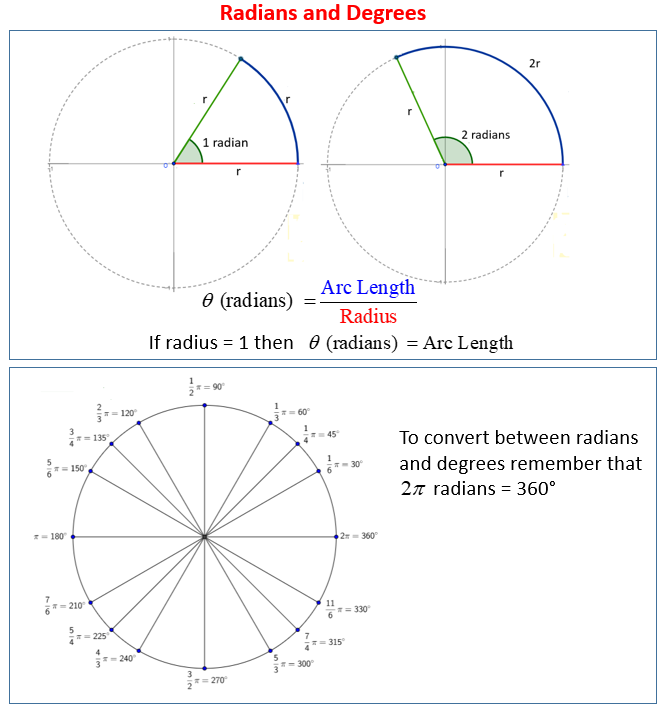
Angles in radians
We can define radian in terms of the arc length and the radius:
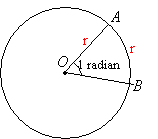
The size of an angle in radian is given by the ratio of the arc length to the length of the radius.
An angle with 1 radian will have an arc length that is equal to the length of the radius.
An angle with 2 radians will have an arc length that is twice the length of the radius.
How to define radian in terms of the arc length and the radius?
How to convert from degrees to radians. and vice versa?
We can also define radian in terms of the unit circle (a circle of radius 1).
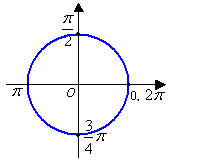
Consider the unit circle whose center is the vertex of the angle to be measured. The angle cuts off an arc of the circle, and the length of that arc is the radian measure of the angle.
How to define radian in terms of the unit circle?It also shows how to convert from degrees to radians.
Convert between degree and radian measurement
We can convert between degree measurement and radian measurement easily.
We know that the circumference of a circle is 2πr. For a unit circle, r = 1 and so the circumference = 2π
This means that 360° equals 2π radians.
Therefore, 1° = 
radians, and 1 radian = 
degrees.
The following are some common angles in both degree measurement and radian measurement.
Worksheet to convert between radians and degrees
Angles in degrees, minutes and seconds
A circle is divided into 360 equal degrees. Degrees may be further divided into minutes and seconds. Each degree is divided into 60 equal parts called minutes. Each minute is further divided into 60 equal parts called seconds.
1° (degree) = 60' (minutes)
1' (minute) = 60'' (seconds)
For example, 34 degrees 26 minutes 51 seconds can be written as 34° 26’ 51’’
Convert between degrees, minutes, seconds and decimal notation
Parts of a degree can also be written in decimal notation.
For example, 60 degrees 30 minutes is 60 and a half degrees which can be written as 60.5°
Example:
Convert 52.4˚ to degrees and minutes.
Solution:
52.4˚ = 52˚ + 0.4˚
= 52˚ + (0.4 × 60)’
= 52˚ 24’
Adding and subtracting degrees, minutes and seconds
How to add angles in degrees, minutes and seconds?It also shows how to convert an angle measured in degrees, minutes and seconds to decimal notation and vice versa.
This video shows how to add and subtract degrees, minutes and seconds.
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.