Quadratic Functions
In these lessons, we will learn
- the different forms of quadratic functions (general, factored and vertex forms)
- how to convert from general form to factored form.
- how to convert from the general form to the vertex form using the vertex formula.
- how to convert from the general form to the vertex form using completing the square.
Related Pages
Quadratic Formula
Graphs Of Quadratic Functions
Factoring Out Common Factors
More Algebra Lessons
Math Worksheets
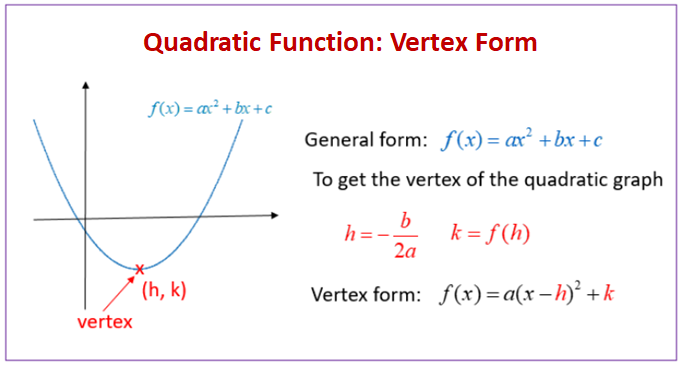
The following diagram shows how to use the vertex formula to convert a quadratic function from general form to vertex form. Scroll down the page for more examples and solutions for quadratic equations.
Forms of Quadratic Functions
We can write quadratic functions in different ways or forms:
- General Form
- Factored Form
- Vertex Form
The general form of a quadratic equation is
y = ax2 + bx + c where a, b and c are real numbers and a is not equal to zero.
For example, y = 2x2 + 5x − 30
The factored form of a quadratic equation is
y = a(x + b)(x + c) where a, b and c are real numbers and a is not equal to zero.
For example, y = 2(x + 6)(x − 5).
The factored form is useful because we can see the x-intercepts (which are also the roots when the function is zero).
For example, the x-intercepts of y = a(x + b)(x + c) are (−b, 0) and (−c, 0)
The vertex form of a quadratic equation is
y = a(x − h)2 + k where a, h and k are real numbers
and a is not equal to zero.
For example, y = 2(x + 6)2 − 5.
The vertex form is useful because we can see the turning point or vertex of the graph.
For example, the turning point or vertex of y = a(x − h)2 + k
is (h, k). If a is positive then it is a minimum vertex. It a is negative then it is a
maximum vertex.
The following video looks at the various formats in which Quadratic Functions may be written as.
General Form to Factored Form
The following videos show how to change quadratic functions from general form to factored form.
General Form to Vertex Form by using the Vertex Formula
We can change a quadratic function from general form to vertex form by using the vertex formula.
Example of how to convert standard form to vertex form of a parabola equation.
General Form to Vertex Form by Completing the Square
We can change a quadratic function from general form to vertex form by completing the square.
The following video shows how to use the method of Completing the Square to convert a quadratic function from standard form to vertex form.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.