The Converse of the Pythagorean Theorem

Related Pages
Pythagorean Theorem
Pythagorean Theorem Word Problems
Applications Of Pythagorean Theorem
More Geometry Lessons

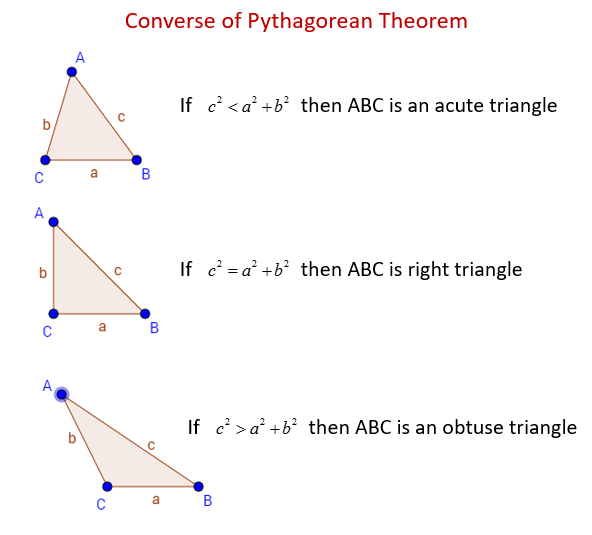
The following figures show the Converse of the Pythagorean Theorem. Scroll down the page for more examples, solutions, and proofs of the Converse of the Pythagorean Theorem.

The Converse of the Pythagorean Theorem

The Pythagorean Theorem states that

In any right triangle, the sum of the squared lengths of the two legs is equal to the squared length of the hypotenuse.

The converse of the Pythagorean Theorem states that

For any triangle with sides a, b, c, if a² + b² = c², then the angle between a and b measures 90° and the triangle is a right triangle.

How to use the converse to determine the type of triangle

We can also use the converse of the Pythagorean theorem to check whether a given triangle is an acute triangle, a right triangle or an obtuse triangle.

For a triangle with sides a, b and c and c is the longest side then:

If c ² < a ² + b ² then it is an acute triangle, i.e. the angle facing side c is an acute angle.

If c ² = a ² + b ² then it is a right triangle, i.e. the angle facing side c is a right angle.

If c ² > a ² + b ² then it is an obtuse triangle, i.e. the angle facing side c is an obtuse angle.

Example:
Determine whether a triangle with sides 3 cm, 5 cm and 7 cm is an acute, right or obtuse triangle.

Solution:
We choose the two shorter sides to be a and b and the longest side to be c.
So a = 3, b = 5 and c = 7.
a ² + b ² = 3² + 5² = 9 + 25 = 34
c² = 7² = 49
49 > 34 → c ² > a ² + b ², and so the triangle is an obtuse triangle.

Example:
Determine whether a triangle with sides 12 cm, 14 cm and 18 cm is an acute, right or obtuse triangle.

Solution:
We choose the two shorter sides to be a and b and the longest side to be c.
So a = 12, b = 14 and c = 18.
a ² + b ² = 12² + 14² = 144 + 196 = 340
c² = 18² = 324
340 < 34 → c ² < a ² + b ², and so the triangle is an acute triangle.

Example:
Determine whether a triangle with sides 8 cm, 15 cm and 17 cm is an acute, right or obtuse triangle.

Solution:
We choose the two shorter sides to be a and b and the longest side to be c.
So a = 8, b = 15 and c = 17.
a ² + b ² = 8² + 15² = 64 + 225 = 289
c² = 17² = 289
289 = 289 → c ² = a ² + b ², and so the triangle is an right triangle.

How to use the converse of the Pythagorean Theorem to determine if a triangle is a right triangle?
Triples to memorize
3-4-5, 5-12-13, 8-15-17, 7-24-25

• Show Video Lesson

How to use the Pythagorean Theorem and its Converse to determine if a triangle is acute, right, or obtuse?
• Use the Pythagorean Theorem to determine if a triangle is acute, right, or obtuse.
• Use the triangle inequality to determine if a triangle can be formed.
The triangle inequality states that in order to construct a triangle, the sum of the shorter sides must be greater than the longest side.

Examples:
Determine if the lengths represent the sides of an acute, right, or obtuse triangle, if a triangle is possible.

1. 7, 24, 25
2. 5, 12, 16
3. 6, 8, 9
4. 3, 5, 9

• Show Video Lesson

The Converse of the Pythagorean Theorem
This video discusses the converse of the Pythagorean Theorem and how to use it verify if a triangle is a right triangle.
Also, two triangle inequalities used to classify a triangle by the lengths of its sides. Both are related to the Pythagorean Theorem.

Example:
Determine if √13, 10 and 12 make a right triangle.

• Show Video Lesson

How to Use the Converse of the Pythagorean Theorem?
How to determine if three given lengths of the sides of a triangle make a right triangle?
This is an application of the Converse of the Pythagorean Theorem.

Example:
The numbers represent the lengths of the sides of a triangle. Classify each triangle as acute, obtuse, or right.
a) 15,20,25
b) 10,15,20

• Show Video Lesson

Converse of Pythagorean Theorem

Examples:

1. Specify all values of x that make the statement true.
   a) ∠1 is an obtuse angel.
   b) The triangle is isosceles.
   c) No triangle is possible.

2. Explain why x must equal 5.
   

3. Explain why ∠D must be a right angle.
   

4. Explain why ∠P must be a right angle.

• Show Video Lesson

Proof of the Converse of the Pythagorean Theorem
The following video will show a proof of the Converse of the Pythagorean Theorem.

• Show Video Lesson

Proof of the Converse of Pythagoras' Theorem

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.