Algebra: Proportion Word Problems

Proportion word problems using algebra involve setting up and solving equations based on proportional relationships between quantities. These problems often require finding an unknown value by setting up a proportion and solving for the variable. Here are some examples of proportion word problems solved using algebra, along with step-by-step solutions.

The following diagrams show the formulas and graphs for direct proportion and inverse proportion problems. Scroll down the page for examples and solutions.

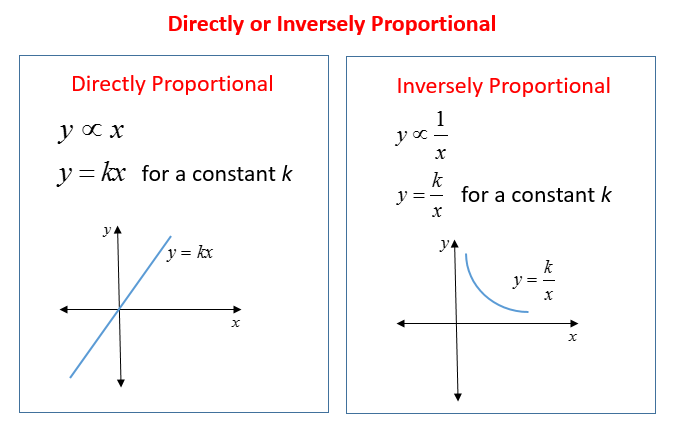
Proportion Word Problems
Direct Proportion Problems
Inverse Proportion Problems
Proportion Word Problems
Ratio & Proportion Problems

Printable & Online Ratio & Proportion Worksheets

Direct Proportion Problems

There are many situations in our daily lives that involve direct proportion.

For example, a worker may be paid according to the number of hours he worked. The two quantities, the number of hours worked (x) and the amount paid (y), are related in such a way that when x changes, y changes proportionately.

In general, when two variables x and y are such that the ratio $\frac{y}{x}$ remains a constant, we say that y is directly proportional to x.

If we represent the constant by k, then we can get the equation:
$\frac{y}{x}$ = k or y = kx where k ≠ 0.

In notation, direct proportion is written as
y ∝ x

Example 1:
If y is directly proportional to x and given y = 9 when x = 5, find:
a) the value of y when x = 15
b) the value of x when y = 6

Solution:
a) Using the fact that the ratios are constant, we get
$\frac{9}{5}$ = $\frac{y}{15}$
⇒ y = $\frac{9}{5}$ × 15
⇒ y = 27

b) $\frac{9}{5}$ = $\frac{6}{x}$
⇒ x = $\frac{5}{9}$ × 6
⇒ x = $\frac{10}{3}$ = $3\frac{1}{3}$

Example 2:
Jane ran 100 meters in 15 seconds. How long did she take to run 2 meter?

Solution:
$\frac{100}{15}$ = $\frac{y}{2}$
⇒ y = $\frac{15}{100}$ × 2
⇒ y = 0.3

Answer: She took 0.3 seconds.

Example 3:
A car travels 125 miles in 3 hours. How far would it travel in 5 hours?

Solution:
$\frac{125}{3}$ = $\frac{y}{5}$
⇒ y = $\frac{125}{3}$ × 5
⇒ y = $208\frac{1}{3}$

Answer: He traveled $208\frac{1}{3}$ miles.

Basic Proportion Problems

Examples:
Use proportions to find the missing value

1. 8 inches in 25 minutes ; 28 inches in x minutes
   
2. 3 gallons in 7 hours ; x gallons in 20 hours

• Show Video Lesson

Proportion Word Problem

Example:
Arthur is typing a paper that is 390 words long. He can type 30 words in a minute. How long will it take for him to type the paper?

• Show Video Lesson

Inverse Proportion Problems

There are also many situations in our daily lives that involve inverse proportion.

For example, the number of days required to build a bridge is inversely proportional to the number of workers. As the number of workers increases, the number of days required to build would decrease.

The two quantities, the number of workers (x) and the number of days required (y), are related in such a way that when one quantity increases, the other decreases.

In general, when two variables x and y are such that
xy = k where k is a non-zero constant, we say that y is inversely proportional to x.

In notation, inverse proportion is written as
y ∝ $\frac{1}{x}$

Example:
Suppose that y is inversely proportional to x and that y = 8 when x = 3. Calculate the value of y when x = 10.

Solution:
Using the fact that the products are constant, we get
3 × 8 = 10y
⇒ y = $\frac{24}{10}$ = $2\frac{2}{5}$

Example:
It takes 4 men 6 hours to repair a road. How long will it take 7 men to do the job if they work at the same rate?

Solution:
4 × 6 = 7y
⇒ y = $\frac{24}{7}$ = $3\frac{3}{7}$

Answer: They will take $3\frac{3}{7}$ hours.

• Show Video Lesson

How To Solve A Word Problem That Involves Inverse Proportion

Examples:

1. Suppose x and y are inversely proportional. If x = 24 and y = 18, then what is x when y = 90?
2. It will take 30 hours for 8 graders to grade all the USAMTS papers. If the graders all grade at the same rate, then how many graders do we need to get the grading done in 12 hours?
3. Ohm’s Law states that current and resistance are inversely proportional. The resistance of a wire is also directly proportional to the length of the wire. If I wish to double the current flowing through a section of a circuit, and all I can change is the length of the wire, then how should I alter the length of the wire?

• Show Video Lesson

Check out many other Algebra Word Problems
Age Word Problems, Average Word Problems, Coin Word Problems, Consecutive Integer Word Problems, Digit Word Problems, Distance Word Problems, Fraction Word Problems, Geometry Word Problems, Integer Word Problems, Interest Word Problems, Lever Word Problems, Mixture Word Problems, Money Word Problems, Motion & Distance Word Problems, Number Sequence Word Problems, Proportion Word Problems, Quadratic Equation Word Problems, Ratio Word Problems, Symbol Word Problems, Variation Word Problems, Work Word Problems.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.