Probability Without Replacement
In these lessons, we will learn how to calculate probability without replacement (dependent events) and how to use a probability tree diagram.
Related Pages
Probability Of An Event
More Lessons On Probability
Probability Tree Diagrams
Dependent Events
What Is Probability Without Replacement Or Dependent Probability?
In some experiments, the sample space may change for the different events. For example, a marble may be taken from a bag with 20 marbles and then a second marble is taken without replacing the first marble. The sample space for the second event is then 19 marbles instead of 20 marbles.
This is called probability without replacement or dependent probability. We can use a tree diagram to help us find the probability without replacement.
How To Find The Probability Without Replacement Or Dependent Probability?
Step 1: Draw the Probability Tree Diagram and write the probability
of each branch. (Remember that the objects are not replaced)
Step 2: Look for all the available paths (or branches) of a
particular outcome.
Step 3: Multiply along the branches and add vertically to find the probability of the outcome.
Example:
A jar consists of 21 sweets. 12 are green and 9 are blue. William picked two sweets at random.
a) Draw a tree diagram to represent the experiment.
b) Find the probability that
i) both sweets are blue.
ii) one sweet is blue and one sweet is green.
c) William randomly took a third sweet. Find the probability that:
i) all three sweets are green?
ii) at least one of the sweet is blue?
Solution:
a) Although both sweets were taken together it is similar to picking one sweet and then the second
sweet without replacing the first sweet.
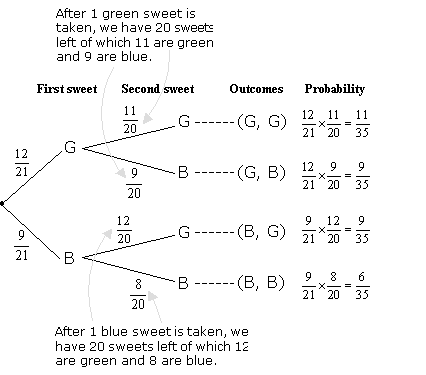
Check that the probabilities in the last column add up to 1.
![]()
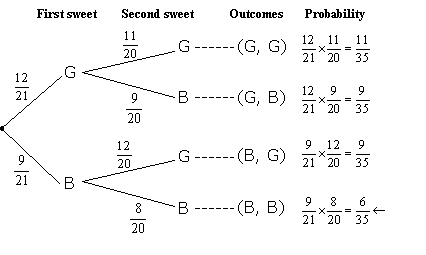
b) i) P(both sweets are blue) = P(B, B)
![]()
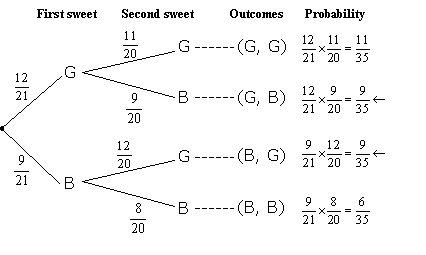
ii) P(one sweet is blue and one sweet is green) = P(G, B) or P(B, G)
![]()
c) i) P(all three sweets are green) = P(G, G, G)
![]()
ii) P(at least 1 sweet is blue) = 1 – P(all three sweets are green)
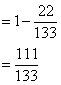
What Is The Difference Between Probability With Replacement (Independent Events) And Probability Without Replacement (Dependent Events) And How To Use A Probability Tree Diagram?
Examples:
-
Adam has a bag containing four yellow gumdrops and one red gumdrop. He will eat one of the gumdrops, and a few minutes later, he will eat a second gumdrop.
a) Draw the tree diagram for the experiment.
b) What is the probability that Adam will eat a yellow gumdrop first and a green gumdrop second?
c) What is the probability that Adam will eat two yellow gumdrops?
d) What is the probability that Adam will eat two gumdrops with the same color?
e) What is the probability that Adam will eat two gumdrops of different colors? -
A jar contains 4 black marbles and 3 red marbles. Two marbles are drawn without replacement.
a) Draw the tree diagram for the experiment.
b) Find probabilities for P(BB), P(BR), P(RB), P(WW), P(at least one Red), P(exactly one red) -
Two marbles are drawn without replacement from a jar containing 4 black and 6 white marbles.
a) Draw the tree diagram for the experiment.
b) Find the probabilities for P(at least one black marble), P(same color), P(BW), P(exactly one black marble)
Probability Question Using Tree Diagrams (Without Replacement)
Example:
A bag contains 5 blue balls and 4 red balls. A ball is picked and not replaced.
What is the probability of picking at least one red ball?
How To Calculate Probability With And Without Replacement?
A visual tutorial on how to calculate probability with and without replacement using marbles.
How To Calculate Probability Without Replacement Or Dependent Probability?
Example:
Andrea has 8 blue socks and 4 red socks in her drawer. She chooses one sock at random and puts it on.
She then chooses another sock without looking.
Find the probability of the following event P(red, then red).
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.