Parent Functions And Their Graphs

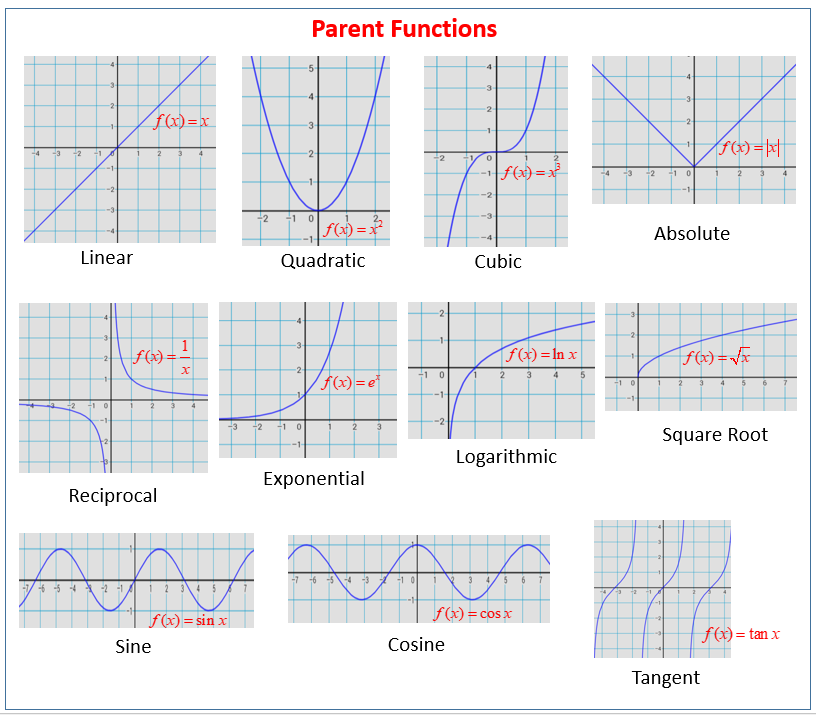
Parent Functions

A parent function is the simplest form of a family of functions. It’s the most basic, unmodified version of a function type, from which all other functions in that family can be derived through transformations (like translations, reflections, stretches, and compressions)

The following figures show the graphs of parent functions: linear, quadratic, cubic, absolute, reciprocal, exponential, logarithmic, square root, sine, cosine, tangent. Scroll down the page for more examples and solutions.

How to use the Parent Functions?
Parent functions help you graph complex functions by:

1. Starting with the parent graph
2. Applying transformations step-by-step

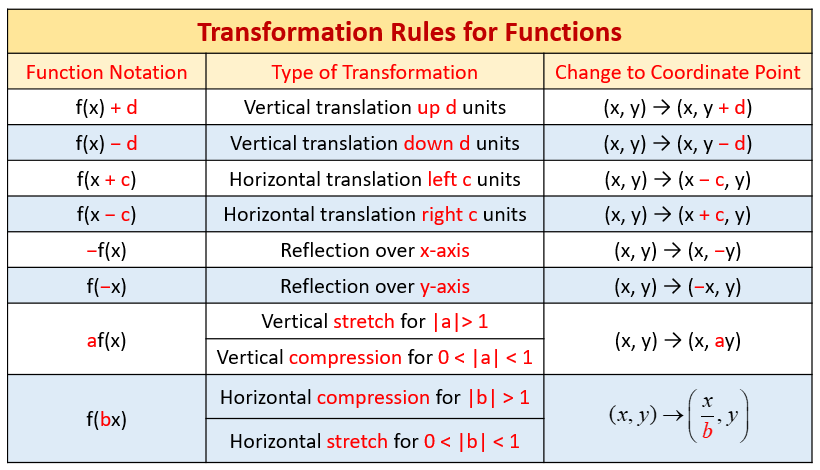
Graphing Transformations
The following table shows the transformation rules for functions. Scroll down the page for examples and solutions on how to use the transformation rules.

Parent Functions And Their Graphs - How To Graph Elementary Functions?

In math, we often encounter certain elementary functions. These elementary functions include rational functions, exponential functions, basic polynomials, absolute values and the square root function. It is important to recognize the graphs of elementary functions, and to be able to graph them ourselves. This will be especially useful when doing transformations.

Basic Graphs That Every Algebra Student Should Know

Basic graphs that are useful to know for any math student taking algebra or higher.
y = mx + b (linear function)
y = x² (quadratic)
y = x³ (cubic)
y = x⁵
y = |x| (absolute)
y = √x (square root)
y = 1/x (reciprocal)
y = 1/x²
y = log_b(x) for b > 1
y = a^x for a > 1 (exponential)
y = a^x for 0 < a < 1

• Show Video Lesson

The Graphs Of Six Basic Functions That You Should Know

f(x) = x
f(x) = x²
f(x) = x³
f(x) = √x
f(x) = cube root(x)
f(x) = |x|

• Show Video Lesson

7 Parent Functions With Equations, Graphs, Domain, Range And Asymptotes

y = x
y = x²
y = √x
y = x³
y = 1/x
y = 1/x²
y = |x|

• Show Video Lesson

Exploring Properties Of Parent Functions

In math, every function can be classified as a member of a family. Each member of a family of functions is related to its simpler, or most basic, function sharing the same characteristics. This function is called the parent function.

This lesson discusses some of the basic characteristics of linear, quadratic, square root, absolute value and reciprocal functions.

Transformations Of Parent Functions

Learn how to shift graphs up, down, left, and right by looking at their equations.

Vertical Shifts:
f(x) + c moves up,
f(x) - c moves down.

Horizontal Shifts:
f(x + c) moves left,
f(x - c) moves right.

• Show Video Lesson

Transforming Graphs And Equations Of Parent Functions

Looking at some parent functions and using the idea of translating functions to draw graphs and write equations.

Here is a list of topics:

1. F(x) functions and transformations
2. Horizontal Shift - Left and Right Units
3. Vertical Shift - Units Up and Down
4. Reflection about the x-axis, y-axis, and origin
5. Inverse function f-1(x)
6. Domain and Range - X and Y Values
7. Horizontal and Vertical Asymptotes
8. End Behavior - Left and Right Side
9. Linear Functions: y=x
10. Parabolas and Quadratic Functions: y=x²
11. Polynomial Functions - Cubic Functions: y=x³
12. Absolute Value Functions
13. Cube Root Functions
14. Square Root and Radical Functions
15. Rational Functions y = 1/x - Vertical and Horizontal Asymptotes
16. Exponential Functions: y=e^x
17. Logarithmic Functions - Log and Natural Log Functions y=lnx
18. Trigonometric Functions - sine, cosine, and tangent - sin cos tan
19. Inverse Trigonometric Functions y = sin^-1 x cos^-1(x) and tan^-1(x)

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.