Mean From Frequency Table With Intervals
Related Pages
Mean From The Frequency Table With Discrete Data
Central Tendency
More Statistics Lessons
In these lessons, we will learn how to find the mean, mode and median from a frequency table for both discrete and grouped data.
How to find the Mean of Grouped Data?
The formula to find the mean of grouped data from a frequency table is given below. Scroll down the page for more examples and solutions.

How To Find The Mean From A Frequency Distribution Table?
The following example shows how to determine the mean from a frequency table with intervals or grouped frequency table.
Example:
The following table shows the frequency distribution of the diameters of 40 bottles.
(Lengths have been measured to the nearest millimeter) Find the mean of the data.
| Diameter (mm) | 35 – 39 | 40 – 44 | 45 – 49 | 50 – 54 | 55 – 60 |
|---|---|---|---|---|---|
| Frequency | 6 | 12 | 15 | 10 | 7 |
Solution:
Step 1: Find the midpoint
of each interval.
Midpoint of interval = ![]() (Lower class limit + Upper class limit)
(Lower class limit + Upper class limit)
= ![]() (39 + 35) = 37
(39 + 35) = 37
| Diameter (mm) | 35 – 39 | 40 – 44 | 45 – 49 | 50 – 54 | 55 – 60 |
|---|---|---|---|---|---|
| Frequency (f) | 6 | 12 | 15 | 10 | 7 |
| Mid-point (x) | 37 | 42 | 47 | 52 | 57 |
Step 2: Multiply the frequency of each interval by its mid-point.
| Diameter (mm) | 35 – 39 | 40 – 44 | 45 – 49 | 50 – 54 | 55 – 60 |
|---|---|---|---|---|---|
| Frequency (f) | 6 | 12 | 15 | 10 | 7 |
| Mid-point (x) | 37 | 42 | 47 | 52 | 57 |
| f × x | 222 | 504 | 705 | 520 | 399 |
Step 3: Get the sum of all the frequencies (f) and the sum of all the fx. Divide ‘sum of fx’ by ‘sum of f ’ to get the mean.
| Total | ||||||
|---|---|---|---|---|---|---|
| Diameter (mm) | 35 – 39 | 40 – 44 | 45 – 49 | 50 – 54 | 55 – 60 | |
| Frequency (f) | 6 | 12 | 15 | 10 | 7 | 50 |
| Mid-point (x) | 37 | 42 | 47 | 52 | 57 | |
| f × x | 222 | 504 | 705 | 520 | 399 | 2350 |
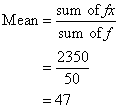
How To Find The Mean, Mode And Median From A Frequency Table For Both Discrete And Grouped Data?
Mean: multiply midpoints by frequencies and add the sub-totals. Divide by the total of the frequencies.
Mode: find the largest frequency - the corresponding value is the modal value or modal class.
Median: calculate a running total of the frequencies - the first interval that is above half the total contains the median.
How To Find The Mean From A Frequency Table For Discrete Data And Continuous (Grouped) Data?
How To Get Averages From Grouped Frequency Tables, Including The Range, Mean, Median And Mode?
How To Work Out The Mean From A Grouped Frequency Table?
First work out the midpoints of each group. Then multiply the midpoints by the frequency. Divide the total of this column by the total frequency.
How to use a TI-84 calculator to calculate the Mean and Standard Deviation of a Frequency Distribution?
Find the mean and the standard deviation of the population data summarized by the following frequency distribution.
How to use a TI-84 calculator to calculate the Mean and Standard Deviation of a Grouped Frequency Distribution?
Find the mean and the standard deviation of the sample data summarized by the following frequency distribution.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.