Maxima and Minima in Calculus
In these lessons, we will learn
- the definition of local maximum and local minimum
- the definition of global maximum and global minimum
- Fermat’s Theorem
- definition of critical number
- the Extreme Value Theorem
- the Closed Interval Method
The local maxima are the largest values (maximum) that a function takes in a point within a given neighborhood.
The local minima are the smallest values (minimum), that a function takes in a point within a given neighborhood.
Definition of local maximum and local minimum
A function f has a local maximum (or relative maximum) at c, if f(c) ≥ f(x) where x is near c.
Similarly, f has a local minimum at c if f(c) ≤ f(x) when x is near c.
Definition of global maximum or global minimum
A function f has a global maximum (or absolute maximum) at c if f(c) ≥ f(x) for all x in D, where D is the domain of f. The number f(c) is called the maximum value of f on D.
Similarly, f has a global minimum (or absolute minimum) at c if f(c) ≤ f(x) for all x in D and the number f(c) is called the minimum value of f on D.
The maximum and minimum values of f are called the extreme values of f
The following diagram illustrates local minimum, global minimum, local maximum, global maximum. Scroll down the page for examples and solutions.
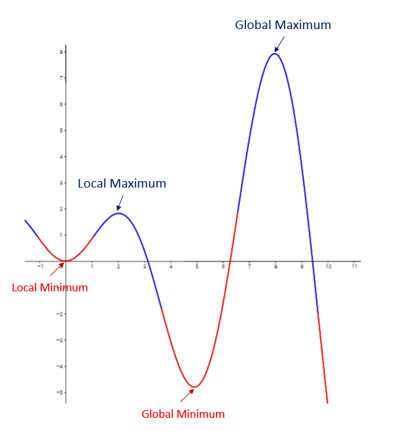
Absolute Extrema
What is absolute maximum and absolute minimum?
Examples:
For each function, determine if f(x) has an absolute max and absolute min on the given interval.
- f(x) = x3 on the Reals
- f(x) = x3 on (1,3]
- f(x) = x2 on the Reals
- f(x) = x2 on [2,4]
Fermat’s Theorem
If f has a local maximum or minimum at c, and if f ‘(c) exists then
f ‘(c) = 0
Definition of critical number
A critical number of a function f is a number c in the domain of f such that either f ‘(c) = 0 of f ‘(c) does not exists.
Example:
Find the critical numbers of ![]()
Solution:
Using the Product Rule, we get
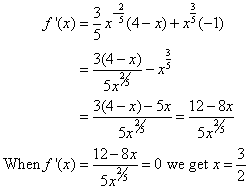
and f ‘(x) does not exist when x = 0.
So, the critical numbers are ![]() and 0.
and 0.
How to find all the critical values of a function?
This video gives the definition of critical numbers and review several examples.
Examples:
Find all critical values of each function.
- f(x) = x2 - 3x + 4
- f(x) = x3 - 4x2 + 5x + 2
- h(x) = 1/x2
- g(x) = xex2
The Extreme Value Theorem
If f is continuous on a closed interval [a, b], then f attains an absolute maximum value f(c) and an absolute minimum value f(d) at some number c and d in [a, b]
Examples of the Extreme Value Theorem
Determine if Extreme Value Theorem applies to f(x) on the specified interval and if so, find the guaranteed absolute maximum and absolute minimum of f(x) on the interval.
- f(x) = x3 on [2,5]
- f(x) = x3 on (2,5]
- f(x) = x2 on (1,2]
- f(x) = 1/x on [-1,1]
- f(x) = 1/x on (1,3)
- f(x) = 1/x on [1,3]
How to use the Extreme Value Theorem to find where the absolute extremum happens?
Example:
- Find the absolute extrema of y = 2x3 - 3x2 - 12x + 5 on the interval [-3, 3]
- Find the absolute extrema of y = exsin(x) on the interval [0,2π]
The Closed Interval Method
These are the steps to find the absolute maximum and minimum values of a continuous function f on a closed interval [a, b]:
Step 1: Find the values of f at the critical numbers of f in (a, b).
Step 2: Find the values of f at the endpoints of the interval.
Step 3: The largest of the values from Steps 1 and 2 is the absolute maximum value and the smallest of these values is the absolute minimum value.
Example
Find the absolute maximum and minimum value of the function
Solution:
Since f is continuous on ![]() , we can use the Closed Interval Method.
, we can use the Closed Interval Method.
Step 1: Find the values of f at the critical numbers of f in ![]()
f(x) = x3 – 3x2 + 1
f ‘(x) = 3x2 – 6x = 3x(x – 2)
When f ‘(x) = 3x(x – 2) we get x = 0 or x = 2
So, the critical numbers are x = 0 and x = 2
The values of f at these critical numbers are
f(0) = 1 and f(2) = –3
Step 2: Find the values of f at the endpoints of the interval.
The values of f at the endpoints of the interval are
![]()
Step 3: The largest of the values from Steps 1 and 2 is the absolute maximum value and the smallest of these values is the absolute minimum value.
Comparing the four numbers, we see that the absolute maximum value is f(4) = 17 and the absolute minimum is f(2) = –3.
How to find absolute extrema via the closed interval method?
How to find the Intervals of Increase/Decrease and Local Max/Mins
The basic idea of finding intervals of increase/decrease as well as finding local maximums and minimums.
Increasing/Decreasing Graphs, Local Maximums/Minimums
This video gives a graph and discusses intervals where the function is increasing and decreasing. It also discuss local maximums and minimums.
Finding Local Maximums/Minimums - Second Derivative Test
How to use the second derivative test to find local maximums and local minimums.
The Closed Interval Method to Find Absolute Maximums and Minimums of continuous functions on closed intervals
This video gives the procedure, gives a short geometric idea as to why this works, and then do a specific example.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.