Types Of Matrices
Related Pages
Singular Matrix
Inverse Matrix
More Lessons On Matrices
In these lessons, we will learn the different types of matrices: row matrix, column matrix, zero matrix or null matrix, square matrix, diagonal matrix, scalar matrix, upper triangular and lower triangular matrices, unit matrix or identity matrix, singular and non-singular matrices, and equal matrices.
What Is A Matrix?
A matrix is a rectangular array of numbers. The size or dimension of a matrix is defined by the number of rows and columns it contains. Matrices is plural for matrix.
What Are The Types Of Matrices?
The following diagrams give some of examples of the types of matrices. Scroll down the page for more examples and explanations.

A matrix may be classified by types. It is possible for a matrix to belong to more than one type.
A row matrix is a matrix with only one row.
Example: E is a row matrix of order 1 × 1
![]()
Example: B is a row matrix of order 1 × 3
![]()
A column matrix is a matrix with only one column.
Example: C is a column matrix of order 1 × 1
![]()
A column matrix of order 2 ×1 is also called a vector matrix.
Example: D is a column matrix of order 2 × 1
![]()
A zero matrix or a null matrix
is a matrix that has all its elements zero.
Example: O is a zero matrix of order 2 × 3
![]()
A square matrix is a matrix with an equal number of rows and
columns.
Example: T is a square matrix of order 2 × 2
![]()
Example: V is a square matrix of order 3 × 3
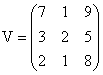
A diagonal matrix is a square matrix that has all its
elements zero except for those in the diagonal from top left to bottom right; which is known
as the leading diagonal of the matrix.
Example: B is a diagonal matrix.
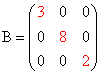
A scalar matrix is a diagonal matrix where all the diagonal
elements are equal.
Example:
\(\left( {\begin{array}{*{20}{c}}3&0&0\\0&3&0\\0&0&3\end{array}} \right)\)
An upper triangular matrix is a square matrix where all the
elements located below the diagonal are zeros.
Example:
\(\left( {\begin{array}{*{20}{c}}2&3&{ - 2}\\0&1&4\\0&0&5\end{array}} \right)\)
A lower triangular matrix is a square matrix where all the elements located above the diagonal are zeros. Example: \(\left( {\begin{array}{*{20}{c}}3&0&0\\{ - 1}&4&0\\2&5&1\end{array}} \right)\)
A unit matrix or identity matrix is a diagonal matrix whose elements in the diagonal are all ones.
Example: P is a unit matrix.
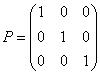
An invertible matrix (Non-singular Matrix) is a square matrix that has an inverse. A matrix is invertible if and only if its determinant is not zero.
An non-invertible matrix (Singular Matrix) is a square matrix that does not have an inverse. Its determinant is zero.
How To Organize Data In Matrices?
Vocabulary: matrix, element, dimension, row matrix, column matrix, square matrix, zero matrix,
equal matrices.
Introduction To Matrices
This video explains the vocabulary used when solving matrices. Rows, Columns, Square Matrix,
Row Matrix, Column Matrix, Zero Matrix, Equal Matrices.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.