Law of Cosines / Cosine Rule
Related Pages
Law Of Sines
Lessons On Trigonometry
More Algebra 2 Lessons
Examples, solutions, and videos to help High School students learn to use the law of cosines.
In this lesson, we will learn:
- the Law of Cosines
- how to use the Law of Cosines when given two sides and an included angle
- how to use the Law of Cosines when given three sides
- how to proof the Law of Cosines
- how to solve applications or word problems using the Law of Cosine
Law of Cosines
The Law of Cosines (also known as the Cosine Rule or Cosine Formula) is a fundamental theorem in trigonometry that relates the lengths of the sides of any triangle to the cosine of one of its angles.
It’s a generalization of the Pythagorean Theorem. The Pythagorean Theorem applies only to right-angled triangles, whereas the Law of Cosines applies to any type of triangles.
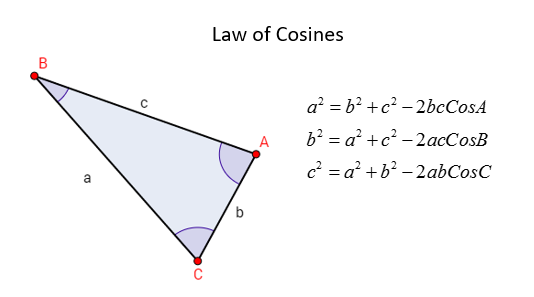
The following diagram shows the Law of Cosines. Scroll down the page if you need more examples and solutions on how to use the Law of Cosines and how to proof the Law of Cosines.
Trigonometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Trigonometry Worksheets
The Law of Cosines Formula
For any triangle with sides a, b, and c, and angles A, B, and C opposite those respective sides:
To find a side:
a2 = b2 + c 2 – 2bc cos A
b2 = a2 + c 2 – 2ac cos B
c2 = a2 + b 2 – 2ab cos C
To find an angle (rearranged from the above formulas):
\(cos(A)= \frac{b^2 + c^2 - a^2}{2bc}\)
\(cos(B)= \frac{a^2 + c^2 - b^2}{2ac}\)
\(cos(C)= \frac{a^2 + b^2 - c^2}{2ab}\)
Key Observation:
Notice that if the angle (e.g., angle C) is 90°, then cos(90°)=0. In this case, the formula c2 = a2 + b 2 – 2ab cos C simplifies to c2 = a2 + b 2, which is the Pythagorean Theorem.
When to Use the Law of Cosines
The Law of Cosines is particularly useful in two main scenarios when solving for unknown sides or angles in any triangle (including non-right triangles):
- Side-Angle-Side (SAS): When you know the lengths of two sides and the measure of the included angle (the angle between those two sides), and you want to find the length of the third side.
- Side-Side-Side (SSS): When you know the lengths of all three sides of a triangle, and you want to find the measure of any of the angles.
If you are given two angles and a side (AAS or ASA) or two sides and a non-included angle (SSA) then use the Law of Sines to solve the triangles.
How to Use the Law of Cosines
The following are some examples of using the Law of Cosines.
Law of Cosines: Given two sides and an included-angle
Example:
Solve triangle PQR in which p = 6.5 cm, q = 7.4 cm and ∠R = 58°.
Solution:
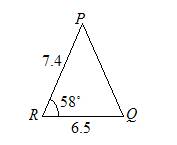
Using the Cosine rule,
r2 = p2 + q2– 2pq cos R
r2 = (6.5)2 + (7.4)2 – 2(6.5)(7.4) cos58°
= 46.03
r = 6.78 cm
Using the Sine rule,

∠Q = 180° – 58° – 54.39°
= 67.61°
∠P = 54.39°, ∠Q = 67.61° and r = 6.78 cm
Law of Cosines: Given three sides
Example:
In triangle ABC, a = 9 cm, b = 10 cm and c = 13 cm. Find the size of the largest angle.
Solution:
The largest angle is the one facing the longest side, i.e. C.
c2 = a2 + b2 – 2ab cos C
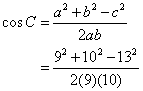
= 0.067
∠C = 86.2°
How to use the cosine rule?
One given SAS and the other given SSS.
Using Law of Cosines to solve triangles given 3 sides (SSS) and 2 sides and the angle in between (SAS).
How to solve an oblique triangle given SSS using the Law of Cosines?
Example:
Solve the triangle using the information given.
a = 3.2, b = 7.6, c = 6.4
Proof of the Law of Cosines
How to prove the law of cosines by using coordinate geometry and the Pythagorean theorem?
Applications using the Law of Cosines
How to solve two word problems using the Law of Cosine?
Example 1:
An engineering firm decides to bid on a proposed tunnel through a mountain. Find how long is the
tunnel and the bid amount.
Example 2:
Find the range of service of a transmission tower.
How to use the Law of Cosines to determine the length across the lake?
Use the Law of Cosines to find the distance a plane has traveled after a change in direction
Example:
A pilot flies in a straight path for 1 h 30 min. She then makes a course correction, heading 8 degrees
to the left and flies 2 h in the new direction. If she maintains a constant speed of 450 mi/h, how far
is she from her starting position?
Use the Law of Cosines to determine the length of a diagonal of a parallelogram
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.