Joint And Combined Variation Word Problems
Related Pages:
Proportions
Proportion Word Problems
Direct Variation
Inverse Variation
More Algebra Lessons
In these lessons, we will learn to solve word problems where a quantity varies in relation to two or more other quantities.
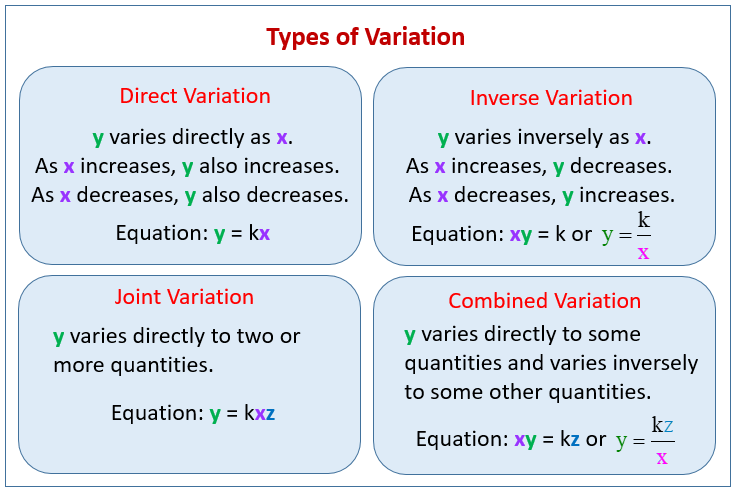
In mathematics, variation describes how one quantity changes in relation to another. There are several types of variation, each with its own unique relationship between variables: Direct Variation, Inverse Variation, Joint Variation, and Combined Variation.
The following diagrams give the different types of variation: Direct Variation, Inverse Variation,
Joint Variation, and Combined Variation. Scroll down the page for examples and solutions.
Ratio & Proportion Worksheets
Practice your skills with the following worksheets:
Printable & Online Proportion Worksheets
In this lesson, we will look at examples for Joint Variation and Combined Variation. Check out the following links for examples other types of variations.
Direct Variation Problems
Inverse Variation Problems
What Is Joint Variation And Combined Variation?
Joint variation is a variation where a quantity varies directly as the product of two or more other quantities.
For example, the area of a rectangle varies whenever its length or its width varies. We say that A ∝ lw, where A is the area, l is the length and w is the width.
Combined variation is a variation where a quantity depends on two (or more) other quantities, and varies directly with some of them and varies inversely with others.
Example 1: A quantity varies inversely as two or more other quantities.
The figure below shows a rectangular solid with a fixed volume. Express its width, w, as a joint variation in terms of its length, l, and height, h.
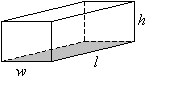
Solution:
\(w \propto \frac{1}{lh}\)
In other words, the longer the length l or the height h, the narrower is the width w.
Example 2: A quantity varies directly as one quantity and inversely as another.
The speed, s, of a moving object varies directly as the distance traveled, d, and varies inversely as the time taken, t. Express s as a joint variation in terms of d and t.
Solution:
s ∝ \(\frac{d}{t}\)
In other words, the longer the distance or the shorter the time, the faster is the speed.
How To Solve Joint Variation Problems?
Example:
Suppose y varies jointly as x and z. What is y when x = 2 and z = 3, if y = 20 when x = 4 and z = 3?
Joint Variation Problems
Example:
z varies jointly with x and y. when x = 3, y = 8, z = 6. Find z, when x = 6 and y = 4.
How to solve Joint Variation Word Problems and Applications?
Example:
The energy that an item possesses due to its motion is called kinetic energy.
The kinetic energy of an object (which is measured in joules) varies jointly with the mass of the
object and the square of its velocity.
If the kinetic energy of a 3 kg ball traveling 12 m/s is 216 Joules, how is the mass of a ball that
generates 250 Joules of energy when traveling at 10 m/s?
Direct, Inverse and Joint Variation
Example:
Determine whether the data in the table is an example of direct, inverse or joint variation. Then,
identify the equation that represents the relationship.
What Is Combined Variation?
In Algebra, sometimes we have functions that vary in more than one element. When this happens, we say that the functions have joint variation or combined variation. Joint variation is direct variation to more than one variable (for example, d = (r)(t)). With combined variation, we have both direct variation and indirect variation.
How to set up and solve combined variation problems?
Example:
Suppose y varies jointly with x and z.
When y = 20, x = 6 and z = 10. Find y when x = 8 and z =15.
Lesson on combining direct and inverse or joint and inverse variation
Example:
y varies directly as x and inversely
as the square of z, and when x = 32, y = 6 and z = 4. Find x when y = 10 and z = 3.
How to solve problems involving joint and combined variation?
Examples:
-
If t varies jointly with u and the square of v, and t is 1152 when u is 8 and v is 4, find t when v is 5 and u is 5.
-
The amount of oil used by a ship traveling at a uniform speed varies jointly with the distance and the square of the speed. If the ship uses 200 barrels of oil in traveling 200 miles at 36 miles per hour, determine how many barrels of oil are used when the ship travels 360 miles at 18 miles per hour.
-
Designer Dolls found that its number of Dress-Up Dolls sold, N, varies directly with their advertising budget, A, and inversely proportional with the price of each doll, P. When $54,00 was spent on advertising and the price of the doll is $90, then 9,600 units are sold. Determine the number of dolls sold if the amount of advertising budget is increased to $144,000.
Combined Variation
Example:
y varies jointly as x and z and inversely as w, and y = 3/2, when x = 2, z =3 and w = 4. Find the equation of variation.
Check out many other Algebra Word Problems
Age Word Problems, Average Word Problems, Coin Word Problems, Consecutive Integer Word Problems, Digit Word Problems, Distance Word Problems, Fraction Word Problems, Geometry Word Problems, Integer Word Problems, Interest Word Problems, Lever Word Problems, Mixture Word Problems, Money Word Problems, Motion & Distance Word Problems, Number Sequence Word Problems, Proportion Word Problems, Quadratic Equation Word Problems, Ratio Word Problems, Symbol Word Problems, Variation Word Problems, Work Word Problems.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.