Sets Intersection: Intersection Of Two Sets
In these lessons, we will learn how to use Venn Diagrams to illustrate the intersection of two sets.
Related Pages
Intersection Of Three Sets
Venn Diagrams
More Lessons On Sets
Venn Diagrams Of Two Sets
The intersection of two sets X and Y is the set of elements that are common to both set X and set Y. It is denoted by X ∩ Y and is read ‘X intersection Y ’.
Example:
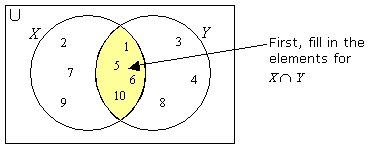
Draw a Venn diagram to represent the relationship between the sets
X = {1, 2, 5, 6, 7, 9, 10} and Y = {1, 3, 4, 5, 6, 8, 10}
Solution:
We find that X ∩ Y = {1, 5, 6, 10} ← in both X and Y
To draw the Venn diagram,
Step 1: Draw two overlapping circles to represent the two sets.
Step 2: Write down the elements in the intersection.
Step 3: Write down the remaining elements in the respective sets.
Notice that you start filling the Venn diagram from the elements in the intersection first.
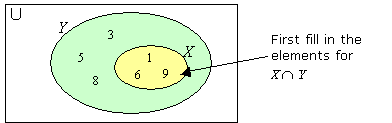
If X ⊂ Y then X ∩ Y = X.
We will illustrate this relationship in the following example.
Example:
Draw a Venn diagram to represent the relationship between the sets
X = {1, 6, 9} and Y = {1, 3, 5, 6, 8, 9}
Solution:
We find that X ∩ Y = {1, 6, 9} which is equal to the set X
For the Venn diagram,
Step 1: Draw one circle within another circle.
Step 2: Write down the elements in the inner circle.
Step 3: Write down the remaining elements in the outer circle.
Venn Diagrams, Unions, And Intersections
Venn diagrams are an important tool allowing relations between sets to be visualized graphically.
This video introduces the use of Venn diagrams to visualize intersections and unions of sets, as well as subsets and supersets.
Intersection Of Sets
Union And Intersection Of Sets
Sets: Union, Intersection, Complement
Example:
U = {7,8,9,10,11,12,13}
A = {8,10,12}, B = {10,12,13}, C = {7,8}
Find
A ∪ B
A ∩ B
A ∪ B'
(A ∪ B') ∩ C
Sets: Union and Intersection
The basic idea of the ‘union’ and ‘intersection’ of two sets.
The intersection of two sets are those elements that belong to both sets.
The union of two sets are all the elements for both sets.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.